题目内容
【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E. 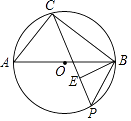
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.
【答案】
(1)证明:∵AB是⊙O的直径,BE⊥CP,
∴∠ACB=∠BEP.
∵∠CAB=∠BPC,
∴△CAB∽△EPB
(2)解:∵AB=10,AC=6,
∴BC= ![]() =8.
=8.
∵△CAB∽△EPB,BP=5,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
∴PE=3,BE=4,
∴CE= ![]() =4
=4 ![]() ,
,
∴CP=4 ![]() +3
+3
【解析】(1)根据两角相等的三角形相似可得出结论;(2)先根据勾股定理求出BC的长,再由相似三角形的性质得出PE及BE的长,由勾股定理得出CE的长,进而可得出结论.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目