题目内容
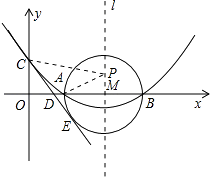
【题目】已知:如图,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于点C,O是坐标原点,已知点B的坐标是(3,0),tan∠OAC=3;
(1)求该抛物线的函数表达式;
(2)点P在x轴上方的抛物线上,且∠PAB=∠CAB,求点P的坐标;
(3)若平行于x轴的直线与抛物线交于点M、N(M点在N点左侧),
①若以MN为直径的圆与x轴相切,求该圆的半径;
②若Q(m,4)是直线MN上一动点,当以点C、B、Q为顶点的三角形的面积等于6时,请直接写出符合条件的m值,为 .
【答案】
(1)
解:∵抛物线y=ax2+bx﹣3与y轴交于点C,
∴点C的坐标为(0,﹣3),
∴OC=3,
∵tan∠OAC=3,
∴OA=1,即点A的坐标为(﹣1,0),
将点A和点B的坐标代入得: ![]() ,解得
,解得 ![]() ,
,
∴抛物线的函数表达式是y=x2﹣2x﹣3
(2)
解:∵∠PAB=∠CAB,
∴tan∠PAB=tan∠CAB=3,
∵点P在x轴上方,设点P的横坐标为x,则点P的纵坐标为3(x+1),
∴3(x+1)=x2﹣2x﹣3,得x=﹣1(舍去)或x=6,当x=6时,y=21,
∴点P的坐标为(6,21)
(3)3或11
【解析】解:(3)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴为直线x=1.
①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
∴R=( R+1﹣1)2﹣4,解得:R= ![]() (负值舍去),
(负值舍去),
∴R= ![]() .
.
当直线MN在x轴下方时,设圆的半径为r(r>0),
∴N(r+1,﹣r),
∴﹣r=(r+1﹣1)2﹣4,解得:r= ![]() (负值舍去),
(负值舍去),
∴r= ![]() ,
,
∴圆的半径为: ![]() 或
或 ![]() .
.
②设直线BC的解析式为y=kx+b,将点C和点B的坐标代入得: ![]() ,
,
解得k=1,b=﹣3,
∴直线BC的解析式为y=x﹣3.
勾股定理可知:BC= ![]() =3
=3 ![]() .
.
∵△QCB的面积为6,
∴BC边上的高线的长度= ![]() =2
=2 ![]() .
.
如图1所示:即直线BC与y=4的交点为D,当点Q在点D的左侧时,过点Q作QE⊥BC,则EQ=2 ![]()

将y=0代入得直线BC的解析式得:x﹣3=4,解得x=7,
∴点D的坐标为(7,4).
∵QD∥x轴,
∴∠QDC=∠OBC=45°.
∴QD= ![]() QE=
QE= ![]() ×2
×2 ![]() =4.
=4.
∴Q(3,4).
∴m=3.
如图1所示,当Q位于点D的右侧时(Q′处),过点Q′作Q′F⊥BC,垂足为F.则FQ=2 ![]() ,
,
同理可知:DQ′=4.
∴点Q′的坐标为(11,4).
∴m=11.
综上所述,m的值为3或11.
所以答案是:3或11.
【考点精析】认真审题,首先需要了解二次函数的概念(一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数).

【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.