题目内容
【题目】已知:菱形ABCD,AB=4m,∠B=60°,点P、Q分别从点B、C同时出发,沿线段BC、CD以1m/s的速度向终点C、D运动,运动时间为t秒.
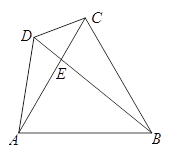
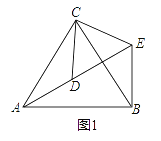
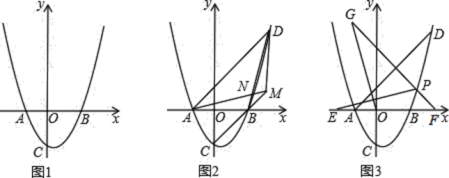
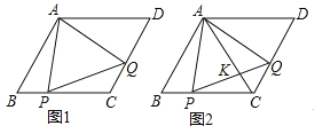
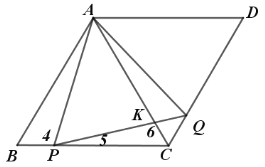
(1)如图1,连接AP、AQ、PQ,试判断△APQ的形状,并说明理由
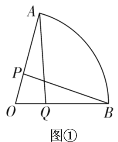
(2)如图2,当t=1.5秒时,连接AC,与PQ相交于点K.求AK的长.
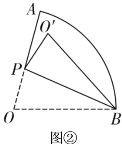
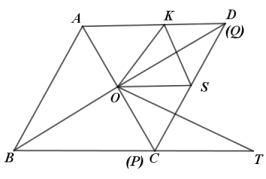
(3)如图3,连接AC交BD于点O,当P、Q分别运动到点C、D时,将∠APQ沿射线CA方向平移,使点P与点O重合,然后以点O为旋转中心将∠APQ旋转一定的角度,使角的两边分别于CD、AD交于S、K点,再以OS为一边在∠SOC内作∠SOT,使∠SOT=∠BDC,OT边交BC的延长线于点T,若BT=4.8,求AK的长.

【答案】(1)等边三角形,见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图1,连接AC,根据菱形的性质证明△ABC和△ACD是等边三角形,得∠B=∠ACQ,AB=AC,由BP=CQ,证明△ABP≌△ACQ,得AP=AQ及∠PAQ=60°,所以△APQ为等边三角形;
(2)由(1)△APQ是等边三角形,由∠4=∠ 6,∠B=∠ACB,得△ABP∽△ PCK,则![]() ,代入数值进行计算,即可得到答案;
,代入数值进行计算,即可得到答案;
(3)由题意先证明△DOS∽△BTO,利用相似三角形的性质,求出DS的长度,然后△AOK∽△ CSO,即可求出AK的长度.
解:(1)△APQ是等边三角形
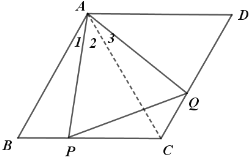
证明:连接AC
∵菱形ABCD
∴AB=BC
∵∠B=60°
∴△ABC是等边三角形
∴AB=AC,①
∵P、Q分别从点B、C同时出发,且速度相同
∴BP=CQ,②
∵菱形ABCD
∴![]() 120°=60°
120°=60°
∴∠ACQ=∠B③
由①②③得△ABP≌△ACQ
∴AP=AQ ,∠1=∠3,
∵∠1+∠2=∠BAC=![]() 120°=60°
120°=60°
∴∠1+∠3=60°=∠PAQ
∴△APQ是等边三角形
(2)由(1)得△APQ是等边三角形
∴∠APQ=60°
∴∠4+∠5=120°
∵∠ACB=60°
∴∠5+∠6=120°
∴∠4=∠ 6,
∵∠B=∠ACB=60°,
∴△ABP∽△ PCK,
∴![]() ,
,
∵当t=1.5秒时,BP=1.5,
∴CP=4![]() 1.5=2.5,
1.5=2.5,
∴![]()
∴![]() ,
,
∴![]() ;
;
(3) ∵菱形ABCD
∴∠BDC=∠DBC=![]()
∵∠SOT=∠BDC
可证△DOS∽△BTO
∴![]()
∵BC=4 ,∠BDC=∠DBC=30°
∴CO=AO=2 ,BO=DO=![]()
∴![]()
∴DS=2.5
∴CS=4![]() 2.5=1.5
2.5=1.5
∵∠DAC=∠KOS=∠ACD
可证∴△AOK∽△ CSO
∴![]()
∴![]()
∴![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案【题目】某通讯经营店销售![]() ,
,![]() 两种品牌儿童手机,今年进货和销售价格如下表:
两种品牌儿童手机,今年进货和销售价格如下表:
|
| |
进货价格(元/只) | 1000 | 1100 |
销售价格(元/只) |
| 1500 |
已知![]() 型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份
型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份![]() 型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
(1)求今年4月份![]() 型手机的销售价是多少元?
型手机的销售价是多少元?
(2)该店计划6月份再进一批![]() 型和
型和![]() 型手机共50部且
型手机共50部且![]() 型手机数量不超过
型手机数量不超过![]() 型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?
型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?