Question

【题目】如图，在直角梯形纸片中，，，，将纸片沿过点的直线折叠，使点落在边上的点处，折痕为．连接并展开纸片．

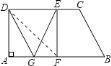
判断四边形的形状，并说明理由．

取线段的中点，连接、，如果，试说明四边形是等腰梯形．

Answer 1

【答案】(1)四边形ADEF为正方形，理由详见解析；（2）详见解析.

【解析】

（1）根据折叠的性质得到∠DEF=∠A=90°，DA=DE，由AB∥DC得∠ADE=90°，则可判断四边形ADEF为矩形，加上邻边相等，由此可判断四边形ADEF为正方形；
（2）由DG∥CB，DC∥AB可判断四边形BGDC是平行四边形，则BC=DG，DC=BG，所以EC≠BG，于是可判断四边形EGBC是梯形，再利用G点为AF的中点和正方形ADEF为轴对称图形得到GE=DG，则EG=CB，所以可判断四边形GBCE是等腰梯形．

四边形为正方形．理由如下：

∵纸片沿过点的直线折叠，使点落在边上的点处，折痕为，

∴，，

∵，

∴，

∴四边形为矩形，

而，

∴四边形为正方形；

∵，，

∴四边形是平行四边形，

∴，，

∴，

∴四边形是梯形，

又∵点为的中点，

∴，

而正方形为轴对称图形，

∴，

∴，

∴四边形为等腰梯形．