题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,添加一个条件,能证明四边形
,添加一个条件,能证明四边形![]() 为正方形的是________.
为正方形的是________.
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() .
.

【答案】①②③
【解析】
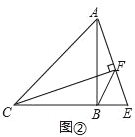
根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC进而得出四边形BECF是菱形;由菱形的性质知,以及菱形与正方形的关系,进而分别分析得出即可.
∵EF垂直平分BC,
∴BE=EC,BF=CF,
∵BF=BE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形;
当①BC=AC时,
∵∠ACB=90°,
则∠A=45°时,菱形BECF是正方形.
∵∠A=45°,∠ACB=90°,
∴∠EBC=45°
∴∠EBF=2∠EBC=2×45°=90°
∴菱形BECF是正方形.
故选项①正确;
当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项②正确;
当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项③正确;
当AC=BF时,无法得出菱形BECF是正方形,故选项④错误.
故答案是:①②③.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目