题目内容
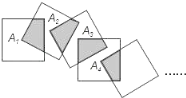
【题目】将 n 个边长都为 1cm 的正方形按如图所示的方法摆放,点 A1,A2,…,An 分别是正方形对角线的交点,则 6 个正方形重叠形成的重叠部分的面积和为( )cm2.
A.![]() B.1C.
B.1C.![]() D.(
D.(![]() )5
)5
【答案】A
【解析】
根据题意可得,阴影部分的面积是正方形的面积的![]() ,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n-1阴影部分的和
,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n-1阴影部分的和
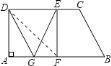
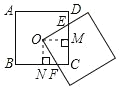
如图,过正方形 ABCD 的中心 O 作 OM⊥CD 于 M,作 ON⊥BC 于N,则∠EOM=∠FON,∠OM=ON,在△OEM 和△OFN 中,
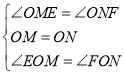 ,
,
∴△OEM≌△OFN(ASA),
则四边形 OECF 的面积就等于正方形 OMCN 的面积,
如正方形 ABCD 的边长是 1,则 OMCN 的面积是![]() ,
,
∴得阴影部分面积等于正方形面积的 ![]() ,即是
,即是![]() ,
,
5 个这样的正方形重叠部分(阴影部分)的面积和为![]() ×4,∴n 个这样的正方形重叠部分(阴影部分)的面积和为
×4,∴n 个这样的正方形重叠部分(阴影部分)的面积和为![]() ×(n﹣1),
×(n﹣1),
∴6 个正方形重叠形成的重叠部分的面积和为![]() ×5=
×5= ![]() . 故选A.
. 故选A.

练习册系列答案
相关题目