Question

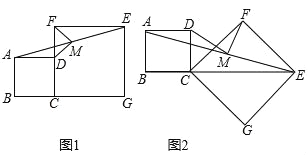
【题目】已知正方形ABCD和正方形CGEF，且D点在CF边上，M为AE中点，连接MD、MF，

（1）如图1，请直接给出线段MD、MF的数量及位置关系是 ；

（2）如图2，把正方形CGEF绕点C顺时针旋转，则（1）中的结论是否成立？若成立，请证明；若不成立，请给出你的结论并证明；

（3）若将正方形CGEF绕点C顺时针旋转30°时，CF边恰好平分线段AE，请直接写出的值．

Answer 1

【答案】(1)MD=MF，MD⊥MF；(2)MD=MF，MD⊥MF仍成立，理由详见解析；(3)．

【解析】

试题分析：（1）延长DM交EF于点P，易证AM=EM，即可证明△ADM≌△EPM，可得DM=PM，根据△DFP是直角三角形即可解题；

（2）延长DM交CE于点N，连接FN、DF，易证∠DAM=∠NEM，即可证明△ADM≌△ENM，可得EN=AD，DM=MN，可证CD=EN，即可证明△CDF≌△ENF，可得DF=NF，即可解题；

（3）根据（1）可得MD=MF，MD⊥MF，若CF边恰好平分线段AE，则CF过点M，最后根据Rt△CDM中，∠DCF=30°，即可求得的值．

试题解析：（1）线段MD、MF的数量及位置关系是MD=MF，MD⊥MF，

理由：如图1，延长DM交EF于点P，

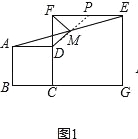
∵四边形ABCD和四边形FCGE是正方形，

∴AD∥EF，∠MAD=∠MEP，∠CFE=90°．

∴△DFP是直角三角形．

∵M为AE的中点，

∴AM=EM．

在△ADM和△EPM中，

∠MAD=∠MEP，AM=EM，∠AMD=∠EMP，

∴△ADM≌△EPM（ASA），

∴DM=PM，AD=PE，

∴M是DP的中点．

∴MF=DP=MD，

∵AD=CD，

∴CD=PE，

∵FC=FE，

∴FD=FP，

∴△DFP是等腰直角三角形，

∴FM⊥DP，即FM⊥DM．

故答案为：MD=MF，MD⊥MF；

（2）MD=MF，MD⊥MF仍成立．

证明：如图2，延长DM交CE于点N，连接FN、DF，

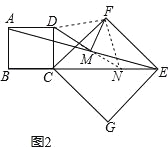
∵CE是正方形CFEG对角线，

∴∠FCN=∠CEF=45°，

∵∠DCE=90°，

∴∠DCF=45°，

∵AD∥BC，

∴∠DAM=∠NEM，

在△ADM和△ENM中，∠MAD=∠NEM，AM=EM，∠AMD=∠EMN，

∴△ADM≌△ENM（ASA），

∴EN=AD，DM=MN，

∵AD=CD，

∴CD=EN，

在△CDF和△ENF中，

CD=EN，∠DCF=∠CEF=45°，CF=EF，

∴△CDF≌△ENF，（SAS）

∴DF=NF，

∴FM=DM，FM⊥DM．

（3）如图所示，若CF边恰好平分线段AE，则CF过点M，

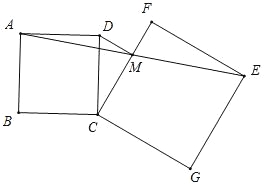
由（1）可得FM=DM，FM⊥DM，

设FM=DM=1，

∵∠DCF=30°，

∴Rt△DCM中，CM=，CD=2=CB，

∴CF=+1=CG，

∴=．