题目内容
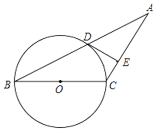
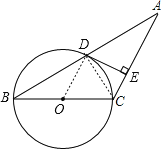
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)若BC=4,求DE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,由平行线的判定定理可得OD∥AC,利用平行线的性质得∠ODE=∠DEA=90°,可得DE为⊙O的切线;
(2)连接CD,由BC为直径,利用圆周角定理可得∠ADC=90°,由∠A=30°,AC=BC=4,利用锐角三角函数可得DE.
(1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠B,
∵AC=BC,
∴∠A=∠B,
∴∠ODB=∠A,
∴OD∥AC,
∴∠ODE=∠DEA=90°,
∴DE为⊙O的切线;
(2)解:连接CD,
∵BC为直径,
∴∠ADC=90°,
∵∠A=30°,
又∵AC=BC=4,
∴AD=ACcos30°=4×![]() =2
=2![]() ,
,
∴DE=![]() AD=
AD=![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目