题目内容
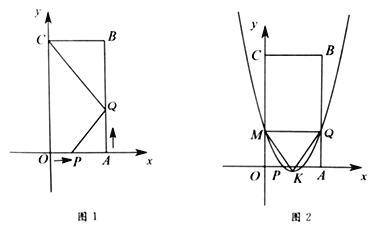
【题目】如图1,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度向点
以每秒2个单位长度的速度向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时运动停止.设运动时间为
重合时运动停止.设运动时间为![]() 秒.
秒.
(1)当![]() 时,线段
时,线段![]() 的中点坐标为________;
的中点坐标为________;
(2)当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
(3)当![]() 时,抛物线
时,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,如图2所示.问该抛物线上是否存在点
,如图2所示.问该抛物线上是否存在点![]() ,使
,使![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
【答案】(1)![]() 的中点坐标是
的中点坐标是![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】(1)先根据时间t=2,和速度可得动点P和Q的路程OP和AQ的长,再根据中点坐标公式可得结论;
(2)根据矩形的性质得:∠B=∠PAQ=90°,所以当△CBQ与△PAQ相似时,存在两种情况:
①当△PAQ∽△QBC时,![]() ,②当△PAQ∽△CBQ时,
,②当△PAQ∽△CBQ时,![]() ,分别列方程可得t的值;
,分别列方程可得t的值;
(3)根据t=1求抛物线的解析式,根据Q(3,2),M(0,2),可得MQ∥x轴,∴KM=KQ,KE⊥MQ,画出符合条件的点D,证明△KEQ∽△QMH,列比例式可得点D的坐标,同理根据对称可得另一个点D.
(1)如图1,∵点A的坐标为(3,0),
∴OA=3,
当t=2时,OP=t=2,AQ=2t=4,
∴P(2,0),Q(3,4),
∴线段PQ的中点坐标为:(![]() ,
,![]() ),即(
),即(![]() ,2);
,2);
故答案为:(![]() ,2);
,2);
(2)如图1,∵四边形OABC是矩形,
∴∠B=∠PAQ=90°
∴当△CBQ与△PAQ相似时,存在两种情况:
①当△PAQ∽△QBC时,![]() ,
,
∴![]() ,
,
4t2-15t+9=0,
(t-3)(t-![]() )=0,
)=0,
t1=3(舍),t2=![]() ,
,
②当△PAQ∽△CBQ时,![]() ,
,
∴![]() ,
,
t2-9t+9=0,
t=![]() ,
,
∵0≤t≤6,![]() >7,
>7,
∴x=![]() 不符合题意,舍去,
不符合题意,舍去,
综上所述,当△CBQ与△PAQ相似时,t的值是![]() 或
或![]() ;
;
(3)当t=1时,P(1,0),Q(3,2),
把P(1,0),Q(3,2)代入抛物线y=x2+bx+c中得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线:y=x2-3x+2=(x-![]() )2-
)2-![]() ,
,
∴顶点k(![]() ,-
,-![]() ),
),
∵Q(3,2),M(0,2),
∴MQ∥x轴,
作抛物线对称轴,交MQ于E,
∴KM=KQ,KE⊥MQ,
∴∠MKE=∠QKE=![]() ∠MKQ,
∠MKQ,
如图2,∠MQD=![]() ∠MKQ=∠QKE,设DQ交y轴于H,
∠MKQ=∠QKE,设DQ交y轴于H,

∵∠HMQ=∠QEK=90°,
∴△KEQ∽△QMH,
∴![]() ,
,
∴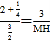 ,
,
∴MH=2,
∴H(0,4),
易得HQ的解析式为:y=-![]() x+4,
x+4,
则 ,
,
x2-3x+2=-![]() x+4,
x+4,
解得:x1=3(舍),x2=-![]() ,
,
∴D(-![]() ,
,![]() );
);
同理,在M的下方,y轴上存在点H,如图3,使∠HQM=![]() ∠MKQ=∠QKE,
∠MKQ=∠QKE,

由对称性得:H(0,0),
易得OQ的解析式:y=![]() x,
x,
则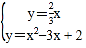 ,
,
x2-3x+2=![]() x,
x,
解得:x1=3(舍),x2=![]() ,
,
∴D(![]() ,
,![]() );
);
综上所述,点D的坐标为:D(-![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).