Question

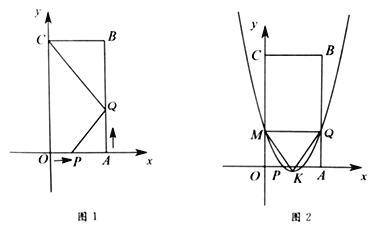
【题目】如图1，图形ABCD是由两个二次函数y1=kx2+m（k＜0）与y2=ax2+b（a＞0）的部分图象围成的封闭图形．已知A（1，0）、B（0，1）、D（0，﹣3）．

（1）直接写出这两个二次函数的表达式；

（2）判断图形ABCD是否存在内接正方形（正方形的四个顶点在图形ABCD上），并说明理由；

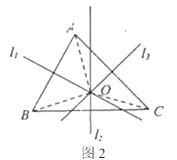
（3）如图2，连接BC，CD，AD，在坐标平面内，求使得△BDC与△ADE相似（其中点C与点E是对应顶点）的点E的坐标

Answer 1

【答案】（1）y1=﹣x2+1，y2=3x2﹣3；（2）存在，理由见解析；（3）（0，﹣）或（，﹣1）或（1，﹣）或（﹣，﹣2）．

【解析】（1）利用待定系数法即可得出结论；

（2）先确定出MM'=（1-m2）-（3m2-3）=4-4m2，进而建立方程2m=4-4m2，即可得出结论；

（3）先利用勾股定理求出AD=，同理：CD=，BC=，再分两种情况：

①如图1，当△DBC∽△DAE时，得出，进而求出DE=，即可得出E（0，-），

再判断出△DEF∽△DAO，得出，求出DF=，EF=，再用面积法求出E'M=，即可得出结论；

②如图2，当△DBC∽△ADE时，得出，求出AE=，

当E在直线AD左侧时，先利用勾股定理求出PA=，PO=，进而得出PE=，再判断出，即可得出点E坐标，当E'在直线DA右侧时，即可得出结论．

（1）∵点A（1，0），B（0，1）在二次函数y1=kx2+m（k＜0）的图象上，

∴，

∴，

∴二次函数解析式为y1=-x2+1，

∵点A（1，0），D（0，-3）在二次函数y2=ax2+b（a＞0）的图象上，

∴，

∴，

∴二次函数y2=3x2-3；

（2）设M（m，-m2+1）为第一象限内的图形ABCD上一点，M'（m，3m2-3）为第四象限的图形上一点，

∴MM'=（1-m2）-（3m2-3）=4-4m2，

由抛物线的对称性知，若有内接正方形，

∴2m=4-4m2，

∴m=或m=（舍），

∵0＜＜1，

∴存在内接正方形，此时其边长为；

（3）在Rt△AOD中，OA=1，OD=3，

∴AD=，

同理：CD=，

在Rt△BOC中，OB=OC=1，

∴BC=，

①如图1，当△DBC∽△DAE时，

∵∠CDB=∠ADO，

∴在y轴上存在E，由，

∴，

∴DE=，

∵D（0，-3），

∴E（0，-），

由对称性知，在直线DA右侧还存在一点E'使得△DBC∽△DAE'，

连接EE'交DA于F点，作E'M⊥OD于M，连接E'D，

∵E，E'关于DA对称，

∴DF垂直平分EE'，

∴△DEF∽△DAO，

∴，

∴，

∴DF=，EF=，

∵S△DEE'=DEE'M=EF×DF=，

∴E'M=，

∵DE'=DE=，

在Rt△DE'M中，DM=

∴OM=1，

∴E'（，-1），

②如图2，

当△DBC∽△ADE时，有∠BDC=∠DAE，，

∴，

∴AE=，

当E在直线AD左侧时，设AE交y轴于P，作EQ⊥AC于Q，

∵∠BDC=∠DAE=∠ODA，

∴PD=PA，

设PD=n，

∴PO=3-n，PA=n，

在Rt△AOP中，PA2=OA2+OP2，

∴n2=（3-n）2+1，

∴n=，

∴PA=，PO=，

∵AE=，

∴PE=，

在AEQ中，OP∥EQ，

∴，

∴OQ=，

∵，

∴QE=2，

∴E（-，-2），

当E'在直线DA右侧时，

根据勾股定理得，AE=，

∴AE'=

∵∠DAE'=∠BDC，∠BDC=∠BDA，

∴∠BDA=∠DAE'，

∴AE'∥OD，

∴E'（1，-），

综上，使得△BDC与△ADE相似（其中点C与E是对应顶点）的点E的坐标有4个，

即：（0，-）或（，-1）或（1，-）或（-，-2）．