��Ŀ����
����Ŀ���Ķ����⣬��������⣺
��ͼ��ʾ��8��8�������ɱ߳�Ϊ1��С��������ɣ�ͼ���е�ͼ����3�����ҹ���������ˬ��ע�⡶�����㾭��ʱ�����ģ����dz���Ϊ����ˬ��ͼ������ˬͨ��������ͼ���иƴ�ӣ���������������ϵ֤���������Ĺ��ɶ��������������ҹ����˶���ѧ�����о���ʹ������ǣ����ҹ���ѧʷ�ϵĽ�����

���⣺
���á���ˬ��ͼ���е��ĸ�ֱ��������ͨ������ѧ����ͼ�α仯����ͼ�ڣ�ͼ�۵ķ���ֽ���������������ͬ��ͼ����ÿ��ֱ�������εĶ�����ڷ���ֽ�ĸ���ϣ����ĸ������λ����ص�����ͼҪ��
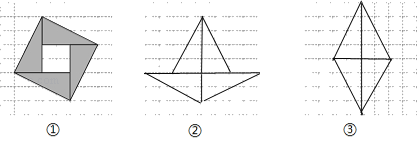
��1��ͼ��������Ƶ�ͼ������������ֽ����������Գ�ͼ�ε��������ĶԳ�ͼ�Σ�
��2��ͼ��������Ƶ�ͼ������������ֽ�����������Գ�ͼ�Σ��������ĶԳ�ͼ�Σ�
���𰸡���1�������� ��2��������
��������
��1��ÿ��ֱ�������εĶ�����ڷ���ֽ�ĸ���ϣ����ĸ������β��ص�������Գ�ͼ�Σ�
��2������Ƶ�ͼ������������ֽ�����������ĶԳ�ͼ�λ���Գ�ͼ�λ���ͼ��
�⣺��1��ͼ������Գ�ͼ�ζ��������ĶԳ�ͼ�Σ�
��2����ͼ�ۼ�����Գ�ͼ�Σ��������ĶԳ�ͼ�Σ�

��ϰ��ϵ�д�
 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д�
�����Ŀ