题目内容
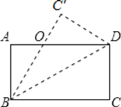
【题目】如图，正方形ABCD中，对角线AC、BD交于点O，将BD绕点B逆时针旋转30°到BE所在的位置，BE与AD交于点F，分别连接DE、CE．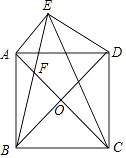
（1）求证：DE=DF；
（2）求证：AE∥BD；
（3）求tan∠ACE的值．
【答案】
（1）
证明：∵BD绕点B逆时针旋转30°到BE，
∴∠DBE=30°，BD=BE，
∴∠BDE=∠BED= 
=75°，
在正方形ABCD中，BD是对角线，
∴∠ADB=45°，
∴∠EDF=75°﹣45°=30°，
在△DEF中，∠DFE=180°﹣∠EDF﹣∠FED=180°﹣30°﹣75°=75°，
∴∠DFE=∠DEF，
∴DE=DF
（2）
证明：过E作EG⊥BD于点G，
∵∠DBE=30°，
∴EG= 
BE= BD，
在正方形ABCD中，AC、BD是对角线，
∴AC=BD，OA= AC= BD，AC⊥BD，
∴EG=OA，且EG∥OA，
∴四边形AOGE是平行四边形，
∵∠AOD=90°，
∴四边形AOGE是矩形，
∴AE∥BD：
（3）
设EG=x，则BE=BD=AC=2EG=2x，
Rt△BEG中，BG= 
= 
x，
∴OG=BG﹣BO=（ ﹣1）x，
在矩形AOGE中，∠EAO=90°
∴AE=OG=（ ﹣1）x，
∴tan∠ACE= 
= 
．
【解析】（1）先根据旋转的性质得∠DBE=30°，BD=BE，求∠BDE=∠BED=75°，则∠EDF=75°﹣45°=30°，根据三角形的内角和得：∠DFE=75°，所以∠DFE=∠DEF，由等角对等边得结论；（2）如图所示，作辅助线，构建直角三角形，根据直角三角形30°角的性质得：EG= BE= BD，由正方形的性质得：AC=BD，OA= AC= BD，根据一组对边平行且相等的四边形是平行四边形证明四边形AOGE是平行四边形，则AE∥BD；（3）证明四边形AOGE是矩形，设EG=x，由勾股定理得：BG= = x，由矩形AOGE可知：∠EAO=90°，计算tan∠ACE的值即可．
【考点精析】利用三角形三边关系和正方形的性质对题目进行判断即可得到答案，需要熟知三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
