题目内容
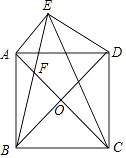
【题目】若 a、b、c 为△ABC 的三边,且满足 a2+b2+c2=ab+ac+bc.点 D 是 AC边的中点,以点 D 为顶点作∠FDE=120°,角的两边分别与直线 AB 和 BC 相交于点 F 和点 E
(1)试判断△ABC 的形状,说明理由
(2)如图 1,将△ABC 图形中∠FDE=120°绕顶点 D 旋转,当两边 DF、DE 分别与边 AB 和射线BC 相交于点 F、E 时,三线段 BE、BF、AB 之间存在什么关系?证明你的结论
(3)如图 2,当角两边 DF、DE 分别与射线 AB 和射线 BC 相交两点 F、E 时,三线段 BE、BF、AB 之间存在什么关系

【答案】(1) △ABC为等边三角形,理由见详解;(2)3AB=2(BE+BF),证明见详解;
(3)3AB=2(BE-BF).
【解析】
(1) a2+b2+c2=ab+ac+bc,等式两边同时乘以2,可得![]() ,可得△ABC为等边三角形;
,可得△ABC为等边三角形;
(2)连接BD,过D点作DG⊥BC,延长BG至H点,使得BG=GH,可证得△BDF≌△HDE,BF=EH,由BH=BE+EH,可得BE、BF、AB 之间的关系;
(3)同理连接BD,过D点作DG⊥BC,延长BG至H点,使得BG=GH,可证得△BDF≌△HDE,BF=EH,由BH=BE-EH,可得BE、BF、AB 之间的关系;
解:(1)由a2+b2+c2=ab+ac+bc,等式两边同时乘以2,可得
2a2+2b2+2c2=2ab+2ac+2bc,可得a2+b2-2ab+ b2 +c2-2bc+ b2+c2-2ac=0
![]()
![]() ,
,![]() a=b=c,
a=b=c,
![]() △ABC为等边三角形;
△ABC为等边三角形;
(2) 如图: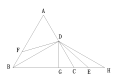
连接BD,,过D点作DG⊥BC,延长BG至H点,使得BG=GH,
易得DG为线段BH点的中垂线,![]() BD=DH
BD=DH
易得∠DBC=∠ABD=30![]() ,
,![]() ∠H=30
∠H=30![]() ,∠BDH=120
,∠BDH=120![]() ,
,
![]() ∠FDE=120°,∠BDE为∠FDE与∠BDH的公共角
∠FDE=120°,∠BDE为∠FDE与∠BDH的公共角
![]() ∠BDF=∠EDH,
∠BDF=∠EDH,
在△BDF与△EDH中,
∠ABD=∠H ;BD=DH;∠BDF=∠EDH
![]() △BDF≌△HDE
△BDF≌△HDE
![]() BF=EH,
BF=EH,
又AD=DC=![]() AC=
AC=![]() AB, ∠ACB=60
AB, ∠ACB=60![]()
![]() GC=
GC=![]() DC=
DC=![]() AB,
AB,
![]() BG= AB -
BG= AB -![]() AB=
AB=![]() AB
AB
![]() BG=GH, BH=BE+EH,
BG=GH, BH=BE+EH,
![]() 2
2![]()
![]() AB=BE+EH,
AB=BE+EH, ![]()
![]() AB= BE+BF,
AB= BE+BF,
即:3AB=2(BE+BF);
(3)如图:
同理连接BD,,过D点作DG⊥BC,延长BG至H点,使得BG=GH,
易得DG为线段BH点的中垂线,![]() BD=DH
BD=DH
可得△BDF≌△HDE
![]() BF=EH
BF=EH
可得:BH=BE-EH,![]()
![]() AB= BE-BF,
AB= BE-BF,
即3AB=2(BE-BF).

【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
| 0.01 | 0.1 | 1 | 10 | 100 |
(2)由上表你发现了什么规律?请用语言叙述这个规律:被开方数扩大_____;
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =______,
=______,![]() =______;
=______;
②已知![]() =0.076 97,则=______.
=0.076 97,则=______.