题目内容
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x+c与y轴交于点A(0,﹣
x+c与y轴交于点A(0,﹣ ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.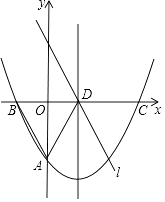
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
解:
【答案】
(1)
解:将A(0,﹣ ![]() )代入抛物线解析式,得c=﹣
)代入抛物线解析式,得c=﹣ ![]() ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() =0化简,得
=0化简,得
x2﹣2x﹣3=0,
∵(x+1)(x﹣3)=0,
∴x1=﹣1,x2=3,
点B(﹣1,0),点C(3,0),
设直线AB的解析式为y=kx+b,将A、B点坐标代入函数解析式,得
![]() ,解得
,解得 ![]() ,
,
直线AB的解析式为y=﹣ ![]() x﹣
x﹣ ![]()
(2)
解:△ABD是等边三角形,
∵点B(﹣1,0),点D(1,0),
∴OB=OD=1,
在△BOA和△DOA中, 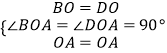 ,
,
∴△BOA≌△DOA,
∴BA=DA.
tan∠ABO= ![]() =
= ![]() =
= ![]() ,
,
∴∠ABO=60°,
∴△ABD是等边三角形
(3)
如图
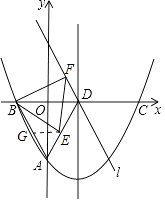 ,
,
过点E作EG∥x轴,交AB于点G,
∵△ABD是等边三角形,
∴∠BAD=∠ABD=∠ADB=60°,
∴∠AEG=∠AGE=60°,
∴△AEG是等边三角形,
∴AE=AG,∴DE=BG.
∵AB∥l,
∴∠EDF=∠BGE=120°,
∴∠GBE+∠GEB=60°,∠DEF+∠GEB=60°,
∴∠GBE=∠DEF,
在△BEG和△EFD中 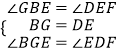 ,
,
∴△BEG≌△EFD,
∴BE=EF,
∵∠BEF=60°,
∴△BEF是等边三角形,
∴S△BEF= ![]() BE2,当BE⊥AD时,BE的长度最小,△BEF的面积最小,
BE2,当BE⊥AD时,BE的长度最小,△BEF的面积最小,
此时BE=ABsin60°= ![]() ,
,
S△BEF最小= ![]() BE2=
BE2= ![]()
【解析】(1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得点的坐标,根据待定系数法,可得函数解析式;(2)根据全等三角形的判定与性质,可得BA与DA,根据正切函数的定义,可得∠ABO,根据等边三角形的判定,可得答案;(3)根据平行线的性质,可得∠AEG=∠AGE=60°,根据全等三角形的判定与性质,可得BE=EF,根据等边三角形的判定,可得△BEF是等边三角形,根据等边三角形的面积,根据垂线段最短,可得BE的长,可得答案.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案