题目内容
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
【答案】
(1)解:A(﹣1,0),B(3,0),C(0,3).
抛物线的对称轴是:直线x=1.
(2)解:①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得: ![]()
解得: ![]() .
.
所以直线BC的函数关系式为:y=﹣x+3.
当x=1时,y=﹣1+3=2,
∴E(1,2).
当x=m时,y=﹣m+3,
∴P(m,﹣m+3).
在y=﹣x2+2x+3中,当x=1时,y=4.
∴D(1,4)
当x=m时,y=﹣m2+2m+3,
∴F(m,﹣m2+2m+3)
∴线段DE=4﹣2=2,
线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m
∵PF∥DE,
∴当PF=ED时,四边形PEDF为平行四边形.
由﹣m2+3m=2,
解得:m1=2,m2=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF与x轴交于点M, 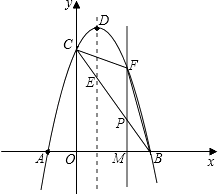
由B(3,0),O(0,0),
可得:OB=OM+MB=3.
∵S=S△BPF+S△CPF
即S= ![]() PFBM+
PFBM+ ![]() PFOM=
PFOM= ![]() PF(BM+OM)=
PF(BM+OM)= ![]() PFOB.
PFOB.
∴S= ![]() ×3(﹣m2+3m)=﹣
×3(﹣m2+3m)=﹣ ![]() m2+
m2+ ![]() m(0≤m≤3).
m(0≤m≤3).
∵B(3,0),C(0,3),D(1,4),
∴ ![]() ,
,
∴ ![]() ,
,
∵∠DEC=∠COB=90°,
∴△DEC∽△COB,
∴∠DCE=∠CBO,
∴∠DCE+∠OCB=90°,
∴DC⊥BC,
∴△BCD的外接圆圆心M为BD中点, 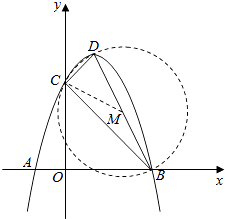
∴MX= ![]() =2,MY=
=2,MY= ![]() =2,
=2,
∴△BCD的外接圆圆心M(2,2)
【解析】(1)与x轴交点令y=0,解方程即可,与y轴交点,令x=0,求出y即可,对称轴可套公式x=![]() ;(2)若四边形PEDF为平行四边形,可得PF∥DE,PF=ED,用m的代数式表示PF,等于DE的长,构建方程即可;(3)用分割的方法把三角形面积分成S△BPF+S△CPF,分别用m的代数式表示底边和高即可.
;(2)若四边形PEDF为平行四边形,可得PF∥DE,PF=ED,用m的代数式表示PF,等于DE的长,构建方程即可;(3)用分割的方法把三角形面积分成S△BPF+S△CPF,分别用m的代数式表示底边和高即可.

【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?