题目内容
【题目】某市居民生活用水实行“阶梯水价”收费,具体收费标准见下表:
每户每月用水量 | 水的价格(单位:元/吨) |
不超过20吨的部分 | 1.6 |
超过20吨且不超过30吨的部分 | 2.4 |
超过30吨的部分 | 3.3 |
例:甲用户1月份用水25吨,应缴水费![]() (元).
(元).
(1)若乙用户1月份用水10吨,则应缴水费________元;
(2)若丙用户1月份应缴水费62.6元,则用水________吨;.
(3)若丁用户1、2月份共用水60吨(1月份用水量超过了2月份),设2月份用水![]() 吨,求丁用户1、2月份各应缴水费多少元.(用含
吨,求丁用户1、2月份各应缴水费多少元.(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)16;(2)32; (3) 1月份应缴水费![]() 元.当2月份用水量不超过20吨时,应缴水费1.6
元.当2月份用水量不超过20吨时,应缴水费1.6![]() 元;当2月份用水量超过20吨但不超过30吨时,应缴水费
元;当2月份用水量超过20吨但不超过30吨时,应缴水费![]() 元.
元.
【解析】
(1)根据每户每月用水量不超过20时,水费价格为1.6元/吨,可知乙用户1月份用水10吨,则应缴水费:1.6×10,计算即可;(2)由于用水30吨时应缴水费为:1.6×20+2.4×10=56<62.6,所以丙用户1月份用水超过30吨,列出方程,求解即可;(3)由丁用户1、2两个月共用水60吨,设2月份用水![]() 吨,则1月份用水(60-a)吨,根据1月份用水量超过了2月份,得出1月份用水量超过了2月份,得出1月份用水量大于30吨,2月份用水量小于30吨,根据三级收费求出1月份应缴水费,分两种情况求出2月份应缴水费,①当2月份用水量不超过20吨时;②当2月份用水量超过20吨但不超过30吨时;
吨,则1月份用水(60-a)吨,根据1月份用水量超过了2月份,得出1月份用水量超过了2月份,得出1月份用水量大于30吨,2月份用水量小于30吨,根据三级收费求出1月份应缴水费,分两种情况求出2月份应缴水费,①当2月份用水量不超过20吨时;②当2月份用水量超过20吨但不超过30吨时;
解:(1)依题意得:1.6×10=16;
故答案为:16
(2) 依题意得:由于用水30吨时应缴水费为:1.6×20+2.4×10=56<62.6,所以丙用户1月份用水超过30吨,设用水为x吨,依题意得:![]()
解得:x=32
故答案为:32;
(3)因为1月份用水量超过了2月份,所以1月份用水量超过了30吨,2月份用水量少于30吨.1月份应缴水费![]() 元.
元.
①当2月份用水量不超过20吨时,应缴水费1.6![]() 元;
元;
②当2月份用水量超过20吨但不超过30吨时,应缴水费![]() 元.
元.

【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
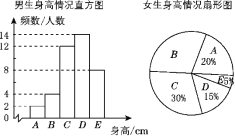
根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.
【题目】甲、乙两台机床同时生产一种零件,在5天中,两台机床每天出次品的数量如下表:
甲 | 0 | 1 | 2 | 0 | 2 |
乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差,说法不正确的是
A. 甲、乙的平均数相等B. 甲、乙的众数相等
C. 甲、乙的中位数相等D. 甲的方差大于乙的方差
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, AC=4.5cm. M是边AC上的一个动点,连接MB,过点M作MB的垂线交AB于点N. 设AM=x cm,AN=y cm.(当点M与点A或点C重合时,y的值为0)
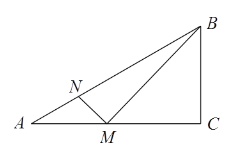
探究函数y随自变量x的变化而变化的规律.
(1) 通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
(要求:补全表格,相关数值保留一位小数)
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当AN=![]() AM时,AM的长度约为 cm(结果保留一位小数).
AM时,AM的长度约为 cm(结果保留一位小数).