��Ŀ����
����Ŀ����֪����ͼ1����A��O��B������ֱ��MN�ϣ��ֽ�����OA�Ƶ�O��˳ʱ�뷽����ÿ��2����ٶ���ת��ͬʱ����OB�Ƶ�O����ʱ�뷽����ÿ��4����ٶ���ת����ͼ2������תʱ��Ϊt��0���t��90�룩��
��1���ú�t�Ĵ���ʽ��ʾ��MOA�Ķ�����
��2�����˶������У�����AOB�ڶ��δﵽ60��ʱ����t��ֵ��
��3������ת�������Ƿ����������t��ʹ������OB��������OM������OA������ON�е�����������ɵĽǣ�ָ����0���������180��Ľǣ���ƽ���ߣ�������ڣ���ֱ��д��t��ֵ����������ڣ���˵�����ɣ�
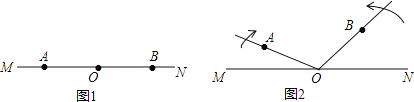
���𰸡���1����MOA=2t����2��t=40��ʱ����AOB�ڶ��δﵽ60�㣻��3����t��ֵ�ֱ�Ϊ18��22.5��36��60��67.5��ʱ������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���ߣ�
��������
�����������1����AOM�Ķ�������OA��ת�ٶȳ�����תʱ�䣻
��2������AOB�ڶ��δﵽ60��ʱ������OB��OA����࣬������AOM+��BON����MON=60���з������ɵã�
��3������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���������������
��OB����ƽ����AOMʱ������![]() ��AOM=��BOM���з�����⣬
��AOM=��BOM���з�����⣬
��OB����ƽ����MONʱ��������BOM=![]() ��MON���з�����⣬
��MON���з�����⣬
��OBƽ����AONʱ��������BON=![]() ��AON���з�����⣮
��AON���з�����⣮
�⣺��1����MOA=2t��
��2����ͼ��
��������֪����AOM=2t����BON=4t��
����AOB�ڶ��δﵽ60��ʱ����AOM+��BON����MON=60����
��2t+4t��180=60����ã�t=40��
��t=40��ʱ����AOB�ڶ��δﵽ60�㣻
��3������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ�������������������
��OBƽ����AOMʱ����![]() ��AOM=��BOM��
��AOM=��BOM��
��t=180��4t����t=4t��180��
��ã�t=36��t=60��
��OBƽ����MONʱ���ߡ�BOM=![]() ��MON������BOM=90����
��MON������BOM=90����
��4t=90����4t��180=90��
��ã�t=22.5����t=67.5��
��OBƽ����AONʱ���ߡ�BON=![]() ��AON��
��AON��
��4t=![]() ��180��2t������180����4t��180��=
��180��2t������180����4t��180��=![]() ��180��2t����
��180��2t����
��ã�t=18��t=90�����������⣬��ȥ����
���ϣ���t��ֵ�ֱ�Ϊ18��22.5��36��60��67.5��ʱ������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���ߣ�

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�