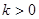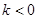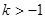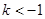题目内容
如图，在平面直角坐标系中有一正方形AOBC，反比例函数
经过正方形AOBC对角线的交点，半径为（
）的圆内切于△ABC，则k的值为 ．
经过正方形AOBC对角线的交点，半径为（）的圆内切于△ABC，则k的值为 ．4
过正方形对角线交点D，做DN⊥BO，DM⊥AO，设圆心为Q，连接切点HQ，QE，
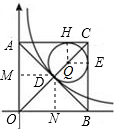
∵在正方形AOBC中，反比例函数y=
经过正方形AOBC对角线的交点，
∴AD=BD=DO=CD，NO=DN，HQ=QE，HC=CE，QH⊥AC，QE⊥BC，∠ACB=90°，
∴四边形HQEC是正方形，∵半径为（4-2
）的圆内切于△ABC，∴DO=CD，
∵HQ2+HC2=QC2，∴2HQ2=QC2=2×（4-2）2，∴QC2=48-32=（4-4）2，
∴QC=4-4，∴CD=4-4+（4-2）=2，∴DO=2，∵NO2+DN2=DO2=（2）2=8，
∴2NO2=8，∴NO2=4，∴DN×NO=4，即：xy=k=4．
∵在正方形AOBC中，反比例函数y=
经过正方形AOBC对角线的交点，∴AD=BD=DO=CD，NO=DN，HQ=QE，HC=CE，QH⊥AC，QE⊥BC，∠ACB=90°，
∴四边形HQEC是正方形，∵半径为（4-2
）的圆内切于△ABC，∴DO=CD，∵HQ2+HC2=QC2，∴2HQ2=QC2=2×（4-2
）2，∴QC2=48-32=（4-4）2，∴QC=4
-4，∴CD=4-4+（4-2）=2，∴DO=2，∵NO2+DN2=DO2=（2）2=8，∴2NO2=8，∴NO2=4，∴DN×NO=4，即：xy=k=4．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
的图象交于点A（4，2），与x轴交于点B．
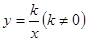的图像经过点
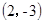，则该函数的图像在 
与函数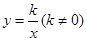
在同一坐标系中的大致图象是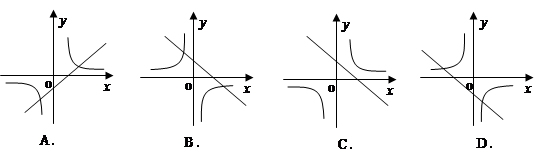
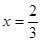代入反比例函数
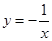中，所得函数值记为
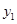，又将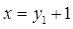
代入反比例函数的关系式中，所得函数值记为
，再将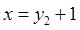
代入反比例函数中，所得函数值记为
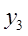，……，如此继续下去，则
＝_____________．
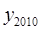上，且OA=4，过A作AC⊥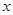
轴于C，OA的垂直平分线交OC于B．则（1）△AOC的面积为 ，（2）△ABC的周长为 .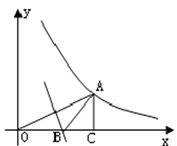
，
、
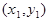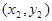为其图象上的两点，若
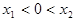时
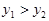，则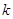
的取值范围是（ ）
