题目内容
如图,直线y=2x﹣6与反比例函数 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.

(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.
 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.
(1)k="8," B点坐标是(3,0)(2)存在, 点C的坐标是(5,0)
解:(1)∵点A(4,2)在反比例函数 的图象上,
的图象上,
∴把(4,2)代入反比例函数 ,得k=8。
,得k=8。
把y=0代入y=2x﹣6中,可得x=3。
∴B点坐标是(3,0)。
(2)存在。
假设存在,设C点坐标是(a,0),则
∵AB=AC,∴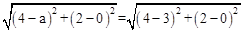 ,即(4﹣a)2+4=5。
,即(4﹣a)2+4=5。
解得a=5或a=3(此点与B重合,舍去)。
∴点C的坐标是(5,0)。
(1)先把(4,2)代入反比例函数解析式,易求k,再把y=0代入一次函数解析式可求B点坐标。
(2)假设存在,设C点坐标是(a,0),然后利用勾股定理可得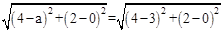 ,
,
解方程,即得a=3或a=5,其中a=3和B点重合,舍去,故C点坐标可求。
 的图象上,
的图象上,∴把(4,2)代入反比例函数
 ,得k=8。
,得k=8。把y=0代入y=2x﹣6中,可得x=3。
∴B点坐标是(3,0)。
(2)存在。
假设存在,设C点坐标是(a,0),则
∵AB=AC,∴
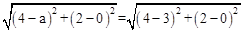 ,即(4﹣a)2+4=5。
,即(4﹣a)2+4=5。解得a=5或a=3(此点与B重合,舍去)。
∴点C的坐标是(5,0)。
(1)先把(4,2)代入反比例函数解析式,易求k,再把y=0代入一次函数解析式可求B点坐标。
(2)假设存在,设C点坐标是(a,0),然后利用勾股定理可得
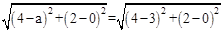 ,
,解方程,即得a=3或a=5,其中a=3和B点重合,舍去,故C点坐标可求。

练习册系列答案
相关题目
 的图像的一个交点为A(-1,n).
的图像的一个交点为A(-1,n).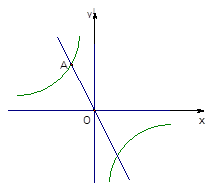
 与一次函数
与一次函数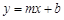 的图象相交于A(1,3),B(n,–1)两点,求反比例函数与一次函数的解析式.
的图象相交于A(1,3),B(n,–1)两点,求反比例函数与一次函数的解析式.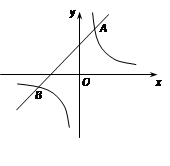
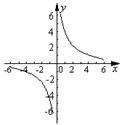
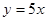
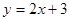
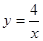
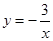
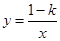 的每一条曲线上,y都随着x的增大而增大,则k的值可以是( )
的每一条曲线上,y都随着x的增大而增大,则k的值可以是( ) (k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足分别为B、C,如果△ABC的面积为3. 则k的值为 .
(k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足分别为B、C,如果△ABC的面积为3. 则k的值为 .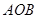 的顶点
的顶点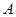 在反比例函数
在反比例函数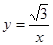 (
(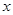 >0)的图象上,则点
>0)的图象上,则点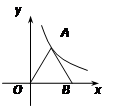
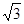 )
)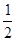 ,
,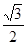 )
) 的图象上,那么y1、y2 、y3的大小关系正确的是 ( )
的图象上,那么y1、y2 、y3的大小关系正确的是 ( )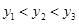

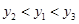
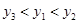
 经过正方形AOBC对角线的交点,半径为(
经过正方形AOBC对角线的交点,半径为( )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 .