题目内容
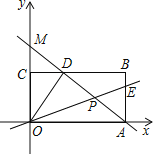
【题目】如图,一次函数y=﹣![]() x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
(1)求m的值及点E、F的坐标;
(2)求△APE的面积;
(3)若B点是x轴上的动点,问在直线EF上,是否存在点Q(Q与A不重合),使△BEQ与△APE全等?若存在,请求出点Q的坐标;若不存在,请说明理由.

【答案】(1)m=![]() ,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(
,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ),Q3(
),Q3(![]() ,﹣2).
,﹣2).
【解析】
(1)根据函数值,可得相应自变量的值,根据自变量的值,可得相应的函数值;
(2)根据待定系数法,可得AP的解析式,根据函数值为零,可得P点坐标,根据三角形的面积公式,可得答案;
(3)分类讨论:①当点A与点B为对应顶点时,根据全等三角形的面积相等,可得Q点的纵坐标,根据函数值,可得相应自变量的值;②当点A与点Q为对应顶点时,可得Q点的纵坐标,根据函数值,可得相应自变量的值.
解:(1)一次函数y=﹣![]() x+4的图象经过点A(m,2),
x+4的图象经过点A(m,2),
得﹣![]() m+4=2,
m+4=2,
解得m=![]() ,
,
∵一次函数y=﹣![]() x+4的图象分别与x轴、y轴的正半轴交于点E,F.
x+4的图象分别与x轴、y轴的正半轴交于点E,F.
∴当y=0时,﹣![]() x+4=0,解得x=3即E(3,0);
x+4=0,解得x=3即E(3,0);
当x=0时,y=4,即F(0,4);
(2)把点A(![]() ,2)一次函数y=kx﹣4,得2=
,2)一次函数y=kx﹣4,得2=![]() k﹣4,解得k=4,
k﹣4,解得k=4,
y=4x﹣4,当y=0时,x=1,即P(1,0).
PE=3﹣1=2,
S△APE=![]() ×2×2=2;
×2×2=2;
(3)存在Q点,B点是x轴上的动点,点Q是直线y=﹣![]() x+4上的点,设Q(m,n).
x+4上的点,设Q(m,n).
由两点间的距离,得AE=![]() =
=![]() ,AP=
,AP=![]() =
=![]() ,PE=2.
,PE=2.
①当点A与点B为对应顶点时,
∵△APE≌△BQE,
∴S△BQE=S△APE=2,
∴![]() BE×|n|=2.
BE×|n|=2.
∵BE=AE=![]() ,
,
∴|n|=![]() ,n=±
,n=±![]() .
.
当n=![]() 时,﹣
时,﹣![]() x+4=
x+4=![]() ,解得m=
,解得m=![]() ,即Q1(
,即Q1(![]() ,
,![]() );
);
当n=﹣![]() 时,﹣
时,﹣![]() x+4=﹣
x+4=﹣![]() ,解得m=
,解得m=![]() ,即Q2(
,即Q2(![]() ,﹣
,﹣![]() );
);
②当点A与点Q为对应顶点时,∵△APE≌△QBE,
则n=﹣2,把n=﹣2代入y=﹣![]() x+4得m=
x+4得m=![]() ,
,
∴Q3(![]() ,﹣2),
,﹣2),
综上所述:Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ),Q3(
),Q3(![]() ,﹣2).
,﹣2).

故答案为:(1)m=![]() ,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(
,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ),Q3(
),Q3(![]() ,﹣2).
,﹣2).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.9千克时,t的值为________________