Question

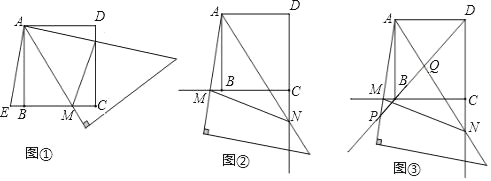
【题目】已知等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕A点旋转时，两边分别交直线BC，CD于点M、N．

（1）如图①，当M、N分别在边BC，CD上时，作AE垂直于AN，交CB的延长线于点E，求证：△ABE≌△ADN；

（2）如图②，当M、N分别在边CB，DC的延长线上时，求证：MN+BM=DN；

（3）如图③，当M、N分别在边CB，DC的延长线上时，作直线BD交直线AM、AN于P、Q两点，若MN=10，CM=8，求AP的长．

Answer 1

【答案】(1)证明见解析；（2）证明见解析；（3）.

【解析】试题分析：由同角的余角相等得到一对锐角相等，再由一对直角相等，又正方形的边长相等，利用ASA即可得到≌

在上截取连接首先证明≌再证为等腰直角三角形，即可得到结论；

连接AC，在中，由MN和CM的长，利用勾股定理求出CN的长，根据图3的结论等量代换即可求出BC的长，从而利用勾股定理求出AC的长，证明 且相似比为 在中，利用勾股定理求出AN的长，代入比例式即可求出AP的长．

试题解析：如图1，

∵AE垂直于AN，

∵四边形ABCD是正方形，

，

又

∴≌（ASA）；

（2）证明：如图②，在上截取连接

∴≌

为等腰直角三角形，

∴AN为MG的垂直平分线，

，即

（3）如图③，连接AC，同（2），证得

即

即，

在中，

根据勾股定理得即

又

在中，

根据勾股定理得

解得