题目内容
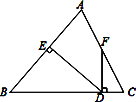
【题目】如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD=DE．
⑴若∠BAE=40°，求∠C的度数；
⑵若△ABC周长13cm，AC=6cm，求DC长．
【答案】（1）35°；（2）3.5cm．
【解析】试题分析：⑴根据垂直平分线的性质易得∠C=∠CAE，AB=AE=EC，由三角形外角的性质可知∠AED=2∠C，再由三角形内角和定理即可求得所求角的度数.
⑵根据△ABC的周长与题中所给条件，可知AB+BC的长度，由⑴中所得相等的边易得
，从而求得DC的长.
试题解析：⑴ ∵AD垂直平分BE，EF垂直平分AC，
∴AB=AE=EC，
∴∠C =∠CAE，∵∠BAE=40°，
∴∠AED =70°，∴
；
⑵ ∵△ABC周长为13 cm，AC=6 cm，
∴AB+BE+EC=7 cm，即2DE+2EC=7 cm，
∴DE+EC=DC=3.5cm．
练习册系列答案
相关题目
