题目内容
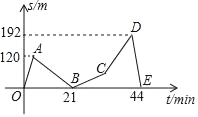
【题目】爸爸和小芳驾车去郊外登山,欣赏美丽的达子香(兴安杜鹃),到了山下,爸爸让小芳先出发6min,然后他再追赶,待爸爸出发24min时,妈妈来电话,有急事,要求立即回去.于是爸爸和小芳马上按原路下山返回(中间接电话所用时间不计),二人返回山下的时间相差4min,假设小芳和爸爸各自上、下山的速度是均匀的,登山过程中小芳和爸爸之间的距离s(单位:m)关于小芳出发时间t(单位:min)的函数图象如图,请结合图象信息解答下列问题:
(1)小芳和爸爸上山时的速度各是多少?
(2)求出爸爸下山时CD段的函数解析式;
(3)因山势特点所致,二人相距超过120m就互相看不见,求二人互相看不见的时间有多少分钟?
【答案】(1)小芳上山的速度为20m/min,爸爸上山的速度为28m/min;(2)爸爸下山时CD段的函数解析式为y=12x﹣288(24≤x≤40);(3)二人互相看不见的时间有7.5分钟.
【解析】分析:(1)根据速度=路程÷时间可求出小芳上山的速度;根据速度=路程÷时间+小芳的速度可求出爸爸上山的速度;
(2)根据爸爸及小芳的速度结合点C的横坐标(6+24=30),可得出点C的坐标,由点D的横坐标比点E少4可得出点D的坐标,再根据点C、D的坐标利用待定系数法可求出CD段的函数解析式;
(3)根据点D、E的坐标利用待定系数法可求出DE段的函数解析式,分别求出CD、DE段纵坐标大于120时x的取值范围,结合两个时间段即可求出结论.
详解:(1)小芳上山的速度为120÷6=20(m/min),
爸爸上山的速度为120÷(21﹣6)+20=28(m/min).
答:小芳上山的速度为20m/min,爸爸上山的速度为28m/min.
(2)∵(28﹣20)×(24+6﹣21)=72(m),
∴点C的坐标为(30,72);
∵二人返回山下的时间相差4min,44﹣4=40(min),
∴点D的坐标为(40,192).
设爸爸下山时CD段的函数解析式为y=kx+b,
将C(30,72)、D(40,192)代入y=kx+b,
![]() ,解得:
,解得:![]() .
.
答:爸爸下山时CD段的函数解析式为y=12x﹣288(24≤x≤40).
(3)设DE段的函数解析式为y=mx+n,
将D(40,192)、E(44,0)代入y=mx+n,
![]() ,解得:
,解得:![]() ,
,
∴DE段的函数解析式为y=﹣48x+2112(40≤x≤44).
当y=12x﹣288>120时,34<x≤40;
当y=﹣48x+2112>120时,40≤x<41.5.
41.5﹣34=7.5(min).
答:二人互相看不见的时间有7.5分钟.