题目内容
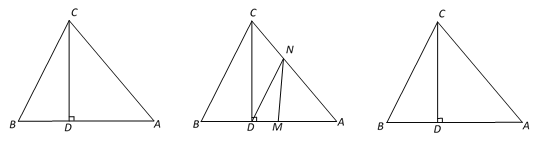
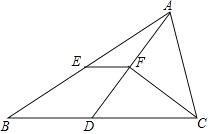
【题目】如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连结EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为3,求△AEF的面积.
【答案】(1)见解析;(2)1
【解析】
(1)依据等腰三角形的性质,即可得到F是AD的中点,再根据三角形中位线定理,即可得到EF∥BC;
(2)依据EF是△ABD的中位线,即可得到EF∥BC,EF:BD=1:2,进而得到S△DEF:S△DEB=1:2,再依据F是AD的中点,即可得出S△DEF=S△AEF=1.
(1)∵DC=AC,CF平分∠ACD,
∴F是AD的中点,
又∵E是AB的中点,
∴EF是△ABD的中位线,
∴EF∥BC;
(2)∵EF是△ABD的中位线,
∴EF∥BC,EF:BD=1:2,
如图,连接DE,则S△DEF:S△DEB=1:2,
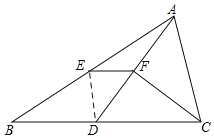
又∵四边形BDFE的面积为3,
∴S△DEF=1,
又∵F是AD的中点,
∴S△DEF=S△AEF=1.

练习册系列答案
相关题目
【题目】某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总成绩 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.