题目内容
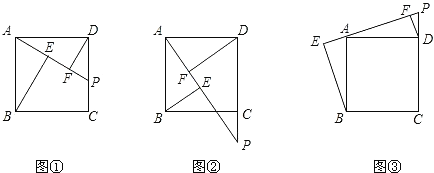
【题目】如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点. 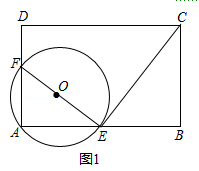
(1)求证:圈O与CE相切与点E;
(2)如图1,若AF=2FD且∠AEF=30°,求n的值; 
(3)如图2.若EF=EC且圈O与边CD相切,求n的值. 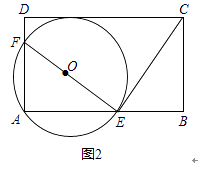
【答案】
(1)证明:在矩形ABCD中,∠A=∠B=90°,
∴圆心O是EF的中点;
∵∠AEF=∠BCE,∠BEC+∠BCE=90°,
∴∠BEC+∠AEF=90°,
即∠FEC=90°,
∴圆O与CE相切与点E
(2)解:如图1,设FD=x,AF=2x;
则BC=3x;
∵∠AEF=30°,
∴AE=AFtan 30°=2 ![]() x,
x,
∵∠BCE=30°,
∴BE=BCtan30°= ![]() x,
x,
∴AB=3 ![]() x,
x,
∴n= ![]() =
= ![]()
(3)解:设切点为G,连OG并延长交AE于点H;
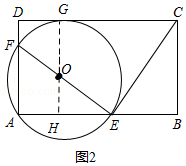
在△AEF与△BCE中,
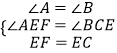
∴△AEF≌△BCE(AAS)
设BC=AE=y,
则BE=AF=(n﹣1)y,
HE= ![]() AE=
AE= ![]() y
y
∴由切线的性质可知:OG=OE=OF,
∴由中位线的性质可知:OH= ![]() AF=
AF= ![]()
∴OE=OG=y﹣ ![]() y=
y= ![]() y,
y,
∴Rt△OHE中,由勾股定理可知:
( ![]() )2=(
)2=( ![]() )2+(
)2+( ![]() )2,
)2,
解得:n= ![]()
【解析】(1)只需要证明∠FEC=90°即可,由于∠AEF=∠BCE,∠BEC+∠BCE=90°,所以∠BEC+∠AEF=90°,(2)设FD=x,AF=2x,所以BC=3x,根据特殊角的锐角三角函数值即可求出BE、AB的长度,从而可求出n的值.(3)设切点为G,连OG并延长交AE于点H;,先证明△AEF≌△BCE,然后根据AB=nAD,可设BC=y,然后用y表示OH、OE,HE的长度,根据勾股定理即可求出n的值.