题目内容
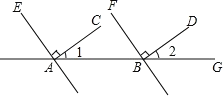
【题目】已知![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() .点
.点![]() 在
在![]() 上(
上(![]() 点与
点与![]() 三点不重合).连接
三点不重合).连接![]() .请你根据题意画出图形并用等式直接写出
.请你根据题意画出图形并用等式直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
【答案】见解析
【解析】
分三种情况,根据平行线的性质及三角形外角的性质求解即可:当点![]() 在线段
在线段![]() 上时,当点P在MB上运动时,当点P在AN上运动时.
上时,当点P在MB上运动时,当点P在AN上运动时.
解:设∠BDP=α、∠ACP=β、∠CPD=γ.
当点![]() 在线段
在线段![]() 上时,∠γ=α+∠β,即
上时,∠γ=α+∠β,即![]() .
.
理由:过点P作PF∥l1(如图1),
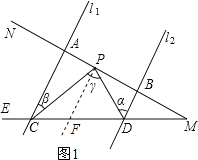
∵l1∥l2,
∴PF∥l2,
∴∠α=∠DPF,∠β=∠CPF,
∴∠γ=∠DPF+∠CPF=α+∠β;
当点P在MB上运动时,∠β=∠γ+∠α,即![]() .
.
理由:如图2,
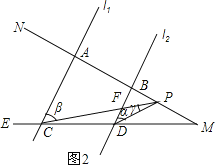
∵l1∥l2,
∴∠β=∠CFD,
∵∠CFD是△DFP的外角,
∴∠CFD=∠α+∠γ
∴∠β=∠γ+∠α;
同理可得,当点P在AN上运动时,∠α=∠γ+∠β,即![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?