题目内容
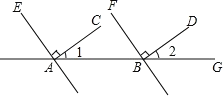
【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
【答案】AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
【解析】
根据同位角相等,两直线平行得到AC∥BD,根据垂直及等量代换得到∠EAB=∠FBG,根据同位角相等,两直线平行证明结论.
因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以AC∥BD(同位角相等,两直线平行).
又因为AC⊥AE(已知),
所以∠EAC=90°.(垂直的定义)
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=125°.
所以∠EAB=∠FBG(等量代换).
所以AE∥BF(同位角相等,两直线平行).
故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.

 阅读快车系列答案
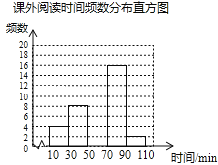
阅读快车系列答案【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?