��Ŀ����
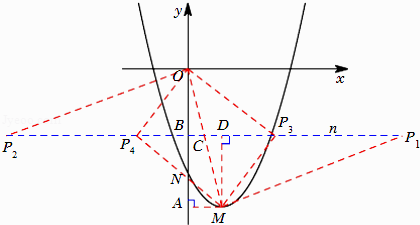
����Ŀ����֪������l��y=ax2+bx+c��a��b��c����Ϊ0���Ķ���ΪM����y��Ľ���ΪN�����dz���NΪ���㣬�Գ�����y���ҹ���M��������Ϊ������l�����������ߣ�ֱ��MNΪ������l������ֱ�ߣ�
��1����ͼ��������y=x2��2x��3�����������ߵĽ���ʽ�� �� ����ֱ�ߵĽ���ʽ����
��2����һ�������ߵ����������ߺ�����ֱ�߷ֱ���y=��2x2+1��y=��2x+1�������������ߵĽ���ʽ��
��3����ͼ���裨1���е�������y=x2��2x��3�Ķ���ΪM����y�ύ��ΪN������������ֱ��MN���Ƶ�N��ת����x��ƽ�У�����y������ƽ��1����λ��ֱ��n��P��ֱ��n�ϵĶ��㣬�Ƿ���ڵ�P��ʹ��POMΪֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��y=��x2��3��y=��x��3
��2��
�⣺�����������ߺ�����ֱ��������ֱ�Ϊԭ�����������������ߵĶ��㣬
�ཫy=��2x2+1��y=��2x+1�������� ![]() ��
��
��� ![]() ��
�� ![]() ��
��
������������y=��2x2+1�Ķ���Ϊ��0��1����
��ԭ�����ߵĶ���Ϊ��1����1����
��ԭ������Ϊy=a��x��1��2��1��
��y=a��x��1��2��1����0��1����
��1=a��0��1��2��1��
��� a=2��
��ԭ������Ϊy=2x2��4x+1��
��3��
�⣺��N��0����3����
��MN�Ƶ�N��ת����x��ƽ�к���ʽΪy=��3��
������y������ƽ��1����λ�õ�ֱ��n����ʽΪy=��2��
���P������x����2����
��O��0��0����M��1����4����
��OM2=��xM��xO��2+��yO��yM��2=1+16=17��
OP2=��|xP��xO|��2+��yO��yP��2=x2+4��
MP2=��|xP��xM|��2+��yP��yM��2=��x��1��2+4=x2��2x+5��
�ٵ�OM2=OP2+MP2ʱ����17=x2+4+x2��2x+5��
���x= ![]() ��x=
��x= ![]() ����P��
����P�� ![]() ����2����P��
����2����P�� ![]() ����2����
����2����
�ڵ�OP2=OM2+MP2ʱ����x2+4=17+x2��2x+5��
��� x=9����P��9����2����
�۵�MP2=OP2+OM2ʱ����x2��2x+5=x2+4+17��
��� x=��8����P����8����2����
������������P�� ![]() ����2����
����2���� ![]() ����2����9����2����8����2��ʱ����POMΪֱ�������Σ�
����2����9����2����8����2��ʱ����POMΪֱ�������Σ�
���������⣺��1����������y=x2��2x��3����0����3����
����������������Ϊy=ax2��3��
��y=x2��2x��3=x2��2x+1��4=��x��1��2��4��
������������Ϊy=ax2��3��������y=x2��2x��3�Ķ��㣨1����4����
�ੁ4=a1��3��
��� a=��1��
������������Ϊy=��x2��3��
������ֱ��Ϊy=kx+b��
��y=kx+b����0����3������1����4����
�� ![]() ��
��
�� ![]() ��
��
������ֱ��Ϊy=��x��3��
�����㾫�������ö��κ�����ͼ��Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�