题目内容
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB=__________时,四边形MENF是正方形(只写结论,不需证明).

【答案】(1)见解析;(2)四边形MENF是菱形.(3)2:1.
【解析】试题分析:(1)根据SAS即可证明△ABM≌△DCM;(2)由(1)得出BM=CM,再根据三角形的中位线定理得出EN=MF,EM=FN,先证四边形MENF是平行四边形,再证ME=MF,从而可得平行四边形MENF是菱形;(3)当AD∶AB=2∶1时,四边形MENF是正方形.可以利用正方形的性质得到MA=AB=MD,从而确定AD:AB的值.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,∴AM=DM,
在△ABM和△DCM,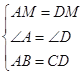
∴△ABM≌△DCM(SAS);
答:四边形MENF是菱形.
证明:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,![]() ,
,
∴NE=FM,NE∥FM,∴四边形MENF是平行四边形,
∵△ABM≌△DCM,
∴BM=CM,
∵E、F分别是BM、CM的中点,
∴ME=MF,
∴平行四边形MENF是菱形;
解:当AD∶AB=2∶1时,四边形MENF是正方形.理由是:
∵四边形MENF是正方形,
∴∠EMF=90°,
由(1)知:Rt△ABM≌Rt△DCM(SAS),
∴∠AMB=∠DMC=45°,
此时MA=MD=DC,
∴AD=2DC,即AD∶AB=2∶1.

【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是


