题目内容
【题目】如图，已知点
，点
是直线上的两点，
厘米，点
，点
是直线上的两个动点，点的速度为1厘米/秒，点的速度为2厘米/秒．点
分别从点，点同时相向出发沿直线运动
秒：
（1）求两点刚好重合时的值；
（2）当两点重合后继续沿原来方向前进，求相距6厘米时的值；
（3）当点离点的距离为2厘米时，求点离点的距离．
【答案】（1）4秒；（2）6秒；（3）7厘米或者5厘米
【解析】
（1）根据题意，两点重合，即相遇，列出等式，即可求解；
（2）根据其速度和相距距离或者路程除以速度列出等式即可；
（3）分两种情况求解：点Q在A点的右边和点Q在A点的左边，即可得解.
（1）因为运动时间为t秒．
由题意，得：t+2t=12，
解得t=4（秒）；
（2）因为运动时间为t秒．
方法一：2（t-4）+（t-4）=6
3t-12=6
t=6（秒）
方法二：t=（12+6）÷（2+1）
t=6（秒）
（3）当点Q离A点的距离为2厘米时，分两种情况：
①点Q在A点的右边，如图所示：
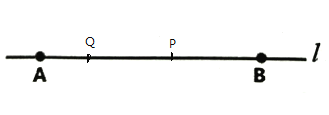
因为AB=12cm
此时，t=(12-2) ÷2=5，
P点经过了5厘米，点P离B点的距离为7厘米；
②点Q在A点的左边，如图所示：
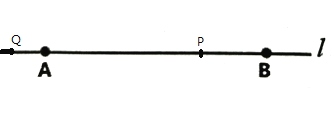
因为点Q运动了(12+2)÷2=7(秒)
此时，t=7，P点经过了7厘米，
所以点P离B点的距离为12-7=5(厘米)．
综上所说，点P离B点的距离为7厘米或者5厘米．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
