题目内容
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=﹣
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=﹣![]() x+2经过点A,C
x+2经过点A,C
(1)求抛物线的解析式;
(2)点P为直线AC上方抛物线上一动点.
①连接PO,交AC于点E,求![]() 的最大值;
的最大值;
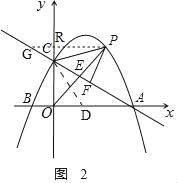
②过点P作PF⊥AC,垂足为点F连接PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①1;②P点坐标是(2,3)或(
x+2;(2)①1;②P点坐标是(2,3)或(![]() ,
,![]() ).
).
【解析】
(1)由直线![]() 求出A、C两点的坐标,代入抛物线的解析式求出
求出A、C两点的坐标,代入抛物线的解析式求出![]() ,
,![]() 的值;
的值;
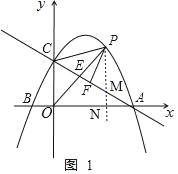
(2)①过点P向![]() 轴做垂线,交直线AC于点M,交
轴做垂线,交直线AC于点M,交![]() 轴于点N,
轴于点N,
利用相似三角形的性质得![]() ,求出
,求出![]() 的表达式,根据一元二次函数的性质,求出
的表达式,根据一元二次函数的性质,求出![]() 的最大值,即可得出答案;
的最大值,即可得出答案;
②分两种情况讨论:
情况一:
以![]() 为条件,由几何关系得出
为条件,由几何关系得出![]() ,即
,即![]() ,
,
令P(![]() ,
,![]() ),代入
),代入![]() 解出P点坐标;
解出P点坐标;
情况二:
以![]() 为条件,
为条件,![]() ,
,
设![]() ,由几何关系得到
,由几何关系得到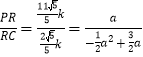 ,解出
,解出![]() 的值,求得P点坐标.
的值,求得P点坐标.
解:(1)当x=0时,y=2,即C(0,2),
当y=0时,x=4,即A(4,0),
将A,C点坐标代入函数解析式,得
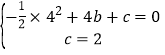 ,
,
解得![]() ,
,
抛物线的解析是![]() ;
;
(2)①过点P向![]() 轴做垂线,交直线AC于点M,交
轴做垂线,交直线AC于点M,交![]() 轴于点N
轴于点N
 ,
,
∵直线![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,即OC=2,
,即OC=2,
设点P(![]() ,
,![]() ),则点M(
),则点M(![]() ,
,![]() ),
),
∴PM=(![]() )-(
)-(![]() )=
)=![]() =
=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值1.
有最大值1.
②∵A(4,0),B(﹣1,0),C(0,2),
∴AC=![]() ,BC=
,BC=![]() ,AB=5,
,AB=5,
∴![]() ,
,
∴△ABC是以∠ACB为直角的直角三角形,取AB的中点D,
∴D(![]() ,0),
,0),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
过P作![]() 轴的平行线交
轴的平行线交![]() 轴于R,交AC的延长线于G,
轴于R,交AC的延长线于G,
情况一:如图,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
令P(![]() ,
,![]() ),
),
∴PR=![]() ,RC=
,RC=![]() ,
,
∴![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,![]() ,P(2,3)
,P(2,3)
情况二,∴![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,
∴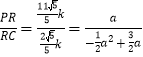 ,
,
∴![]() (舍去),
(舍去),![]() ,
,
![]() ,
,![]() ,即P
,即P![]() ,
,
综上所述:P点坐标是![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.