题目内容
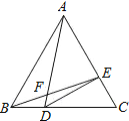
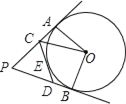
【题目】已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
【答案】(1)12;(2) 65°.
【解析】
(1)根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;
(2)连接OE,根据切线的性质得出∠P+∠AOB=180°,由切线长定理得∠COD= ![]() ∠AOB,即可得出结果.
∠AOB,即可得出结果.
解:(1)∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=6,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA=12;
(2)连接OE,如图所示:
由切线的性质得,OA⊥PA,OB⊥PB,OE⊥CD,
∴∠OAC=∠OEC=∠OED=∠OBD=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°﹣∠P=130°,
由切线长定理得:∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=![]() ∠AOB=
∠AOB=![]() ×130°=65°.
×130°=65°.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目