Question

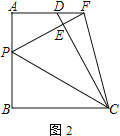
【题目】如图，已知AD∥BC，AB⊥BC，AB＝BC＝4，P为线段AB上一动点．将△BPC沿PC翻折至△EPC，延长CE交射线AD于点D

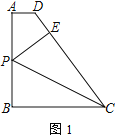
（1）如图1，当P为AB的中点时，求出AD的长

（2）如图2，延长PE交AD于点F，连接CF，求证：∠PCF＝45°

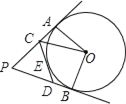
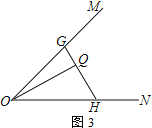
（3）如图3，∠MON＝45°，在∠MON内部有一点Q，且OQ＝8，过点Q作OQ的垂线GH分别交OM、ON于G、H两点．设QG＝x，QH＝y，直接写出y关于x的函数解析式

Answer 1

【答案】（1）1；（2）见解析；（3）

【解析】

(1)如图1.根据平行线的性质得到∠A=∠B=90°，由折叠的性质得到∠CEP=∠B=90°，PB=PE，∠BPC=∠EPC,根据全等三角形的性质得到∠APD=∠EPD,推出 于是得到结论；

(2)如图2.过C作CG⊥AF交AF的延长线于G,推出四边形ABCG是矩形，得到矩形ABCG是正方形，求得CG=CB，根据折叠的性质得到∠CEP=∠B=90°，BC=CE，∠BCP=∠ECP, 根据全等三角形的性质即可得到结论:

(3)如图3，将△OQG沿OM翻折至△OPG,将△OQH沿ON翻折至△ORH,延长PG, RH交于S,推出四边形PORS是正方形，根据勾股定理即可得到结论．

解：（1）如图1，连结，

∵AD//BC. AB⊥BC,

∴∠A=∠B=90°

∵将△BPC沿PC翻折至△EPC,

∴∠CEP=∠B=90°，PB=PE，∠BPC=∠EPC,

∴∠DEP=90°

∵当P为AB的中点，

∴AP=BP

∴PA=PE

∵PD=PD

∴，

∴

作于，设，则，

由勾股定理得，

解得，

∴

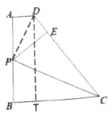
图1

（2）如图2，作交延长线于，易证四边形为正方形

∵∠A=∠B=∠G=90°,

∴四边形ABCG是矩形,

∵AB=BC,

∴矩形ABCG是正方形,

∴CG=CB.

∵将△BPC沿PC翻折至△EPC,

∴∠ FED=90°，CG=CE,

又∵CF=CF

∴，

∴∠ECF=∠GCF,

∴∠BCP+∠GCF=∠PCE+∠FCE=45°

∴∠PCF=45°;

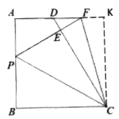
图2/p>

(3)如图3.将△OQG沿OM翻折至OOPG.将△OQH沿ON翻折至△ORH.延长PG, RH交于S,则∠POG=∠QOG.∠ROH=∠QOH, OP=OQ=OR=8,PG=QG=x,QH=RH=y,

∴ ∠POR=2∠MON=90",

∵GH⊥OQ.

∴∠OQG=∠OQH=90° .

∴∠P=∠R=90° ,

∴四边形PORS是正方形。

∴PS=RS=8,∠S=90°，

∴.GS=8-x,HS=8-y.

∴ .

∴

∴

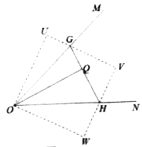
图3