��Ŀ����
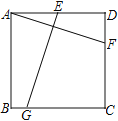
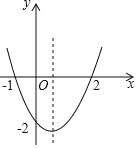
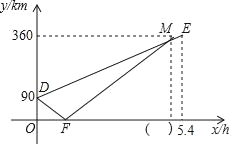
����Ŀ��A��B��C������ͬһ����·�ϣ�A����B��C����֮�䣬�ס�������ͬʱ��A�س���������ʻ���׳�ʻ��C�أ��ҳ���ʻ��B�أ�����B�غ�ͷ��ԭ�پ���A��ʻ��C�أ���ͷʱ����Բ��ƣ�������C��ֹͣ��ʻ���׳����ҳ���0.4Сʱ����C�أ�������B�ص�·��y��km������ʻʱ��x��h��֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ������������⣺
��1���׳���ʻ���ٶ����� ��km/h������ͼ��������������ȷ����ֵ��
��2����ͼ�����߶�FM����ʾ��y��x�ĺ�������ʽ������Ҫд���Ա���x��ȡֵ��Χ����
��3�����ҳ�����C��֮ǰ���ס�������������Сʱ��A��·����ȣ�ֱ��д���𰸣�
���𰸡���1��50��5����2��y��90x��90��1��x��5��;��3��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��
��������
��1���۲�ͼ���ҳ�A��C���ؼ�ľ��룬�ٸ����ٶȣ�·����ʱ�䣬��������׳���ʻ���ٶȣ��ɼ׳����ҳ���0.4Сʱ����C�ؽ�ϼ׳�5.4Сʱ����C�أ��ɵó��ҳ�����C������ʱ�䣻
��2�������ٶȣ�·����ʱ�������ҳ����ٶȣ���ʱ�䣽·�����ٶȿɵó���F�ĺ����꣬�ٸ���·�̣��ٶ�����ʱ�䩁1�������ɵó��߶�FM����ʾ��y��x�ĺ�������ʽ��
��3������·�̣��ٶ���ʱ�䣨·�̣�90���ٶ���ʱ�䣩���ɵó��߶�DM��DF������ʾ��y��x�ĺ�������ʽ����0��x��1�Լ�1��x��5����������ҳ�����x��һԪһ�η��̣���֮���ɵó����ۣ�
�⣺��1��A��C���ؼ�ľ���Ϊ360��90��270��km����
�׳���ʻ���ٶ�Ϊ270��5.4��50��km/h����
�ҳ��ﵽC������ʱ��Ϊ5.4��0.4��5��h����
�ʴ�Ϊ��50��5��
��2���ҵ��ٶ�Ϊ��90+360����5��90��km/h����
��F�ĺ�����Ϊ90��90��1��
���߶�FM����ʾ��y��x�ĺ�������ʽΪy��90��x��1����90x��90��1��x��5����
��3���߶�DE����ʾ��y��x�ĺ�������ʽΪy��50x+90��0��x��5.4����
�߶�DF����ʾ��y��x�ĺ�������ʽΪy��90��90x��0��x��1����
��0��x��1ʱ����90����90��90x����50x+90��90��
��ã�x��0����ȥ����
��1��x��5ʱ����|90x��90��90|��50x+90��90��
��ã�![]()
�����ҳ�����C��֮ǰ���ס�������������![]() Сʱ��
Сʱ��![]() Сʱ��A��·����ȣ�
Сʱ��A��·����ȣ�

 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
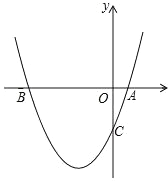
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�����Ŀ��������y��ax2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ�����ʾ��
x | �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
y | �� | ��6 | 0 | 4 | 6 | 6 | �� |
����˵��������������y��Ľ���Ϊ��0��6���� �������ߵĶԳ�����y����Ҳࣻ��������һ�������㣨3��0�������ڶԳ�����࣬y��x�������С��������ʽax2+��b��3��x+c��6��0�⼯Ϊ��2��x��0������˵����ȷ���У�������
A. 1 �� B. 2 �� C. 3 �� D. 4 ��