题目内容
如图，AC=BC，AD=BD，下列结论不正确的是（ ）
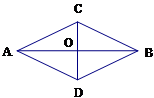
| A．CO=DO | B．AO=BO | C．AB⊥CD | D．△ACO≌△BCO |
A
试题分析：先根据SSS证得△ACD≌△BCD，即得∠ADC=∠BDC，再根据等腰三角形的性质依次分析即可．
在△ACD和△BCD中
AC=BC，AD=BD，CD=CD，
∴△ACD≌△BCD，
∴∠ACD=∠BCD，∠ADC=∠BDC，
∴OA=OB，CD⊥AB（三线合一定理），故选项B、C、D错误；
根据已知不能推出OC=OD，故本选项正确；
故选A．
点评：解答本题的关键是熟练掌握等腰三角形的三线合一的性质：等腰三角形底边上的高、底边上的中线、顶角平分线互相重合.
练习册系列答案
相关题目
BD，E、F、G、H分别为AB、BC、CD、DA的中点.
，
，
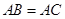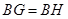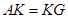，求∠A的度数。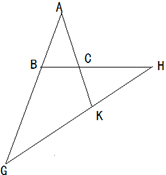
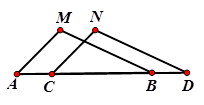
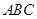，两顶点
分别射线OM,ON上滑动，当∠OAB = 21°时, ∠NBC = 。滑动过程中，连结OC，则OC的长的最大值是 。