题目内容
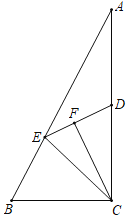
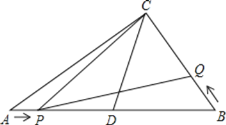
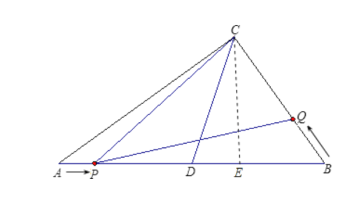
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC、BC的长为方程x2﹣14x+a＝0的两根，且AC﹣BC＝2，D为AB的中点．
（1）求a的值．
（2）动点P从点A出发，以每秒2个单位的速度，沿A→D→C的路线向点C运动；动点Q从点B出发，以每秒3个单位的速度，沿B→C的路线向点C运动，且点Q每运动1秒，就停止2秒，然后再运动1秒…若点P、Q同时出发，当其中有一点到达终点时整个运动随之结束．设运动时间为t秒．
①在整个运动过程中，设△PCQ的面积为S，试求S与t之间的函数关系式；并指出自变量t的取值范围；
②是否存在这样的t，使得△PCQ为直角三角形？若存在，请直接写出所有符合条件的t的值．
【答案】（1）48；（2）① S＝
t2﹣
t+24（0＜t≤1）或S＝﹣t+12（1＜t≤2.5）或S＝﹣t+12（2.5＜t≤3）或S＝t2﹣
t+48（3＜t＜4）；②2.5秒，
秒
【解析】
（1）根据根与系数的关系求出AC+BC=14，求出AC和BC，即可求出答案；
（2）根据勾股定理求出AB，sinB，过C作CE⊥AB于E，关键三角形的面积公式求出CE，I当0＜t≤1时，
求出即可；II同理可求：当1＜t≤2.5时， 
;Ⅲ当2.5＜t≤3时，
;IV当3＜t＜4时
②在整个运动过程中，只可能∠PQC=90°，当P在AD上时，若∠PQC=90°，
，代入即可求出t；当P在DC上时，若∠PQC=90°，sinA=sin∠CPQ，
得到
或
，求出t，根据t的范围1＜t＜4，判断即可．
（1）∵AC、BC的长为方程x2﹣14x+a＝0的两根，
∴AC+BC＝14，
又∵AC﹣BC＝2，
∴AC＝8，BC＝6，
∴a＝8×6＝48，
答：a的值是48．
（2）∵∠ACB=90°
∴
又∵D为AB的中点
∴
∵
过C作CE⊥AB于E，
根据三角形的面积公式得：
6×8=10CE
解得
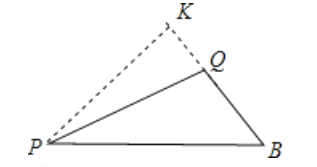
过P作PK⊥BQ于K，
∵
∴
∴
（I）当0<t≤1时，
（II）同理可求：当1<t≤2．5时，
（III）当2．5<t≤3时
（IV）当3<t<4时
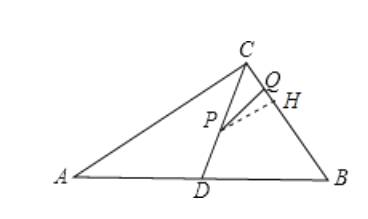
∵△PHC∽△BCA
∴
∴
∴PH=8-1．6t
∴
答：S与t之间的函数关系式是：
或
或
或
② 解：在整个运动过程中，只可能∠PQC=90°
当P在AD上时，若∠PQC=90°，
∴
∴t=2.5
当P在DC上时，若∠PQC=90°
sinA=sin∠CPQ
或
或t=2．5
∵1<t<4
∴t=2.5秒或秒时，△PCQ为直角三角形
答：存在这样的t，使得△PCQ为直角三角形，符合条件的t的值是2.5秒， 秒
