题目内容
【题目】如图,抛物线y=﹣![]() (x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y=
(x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y=![]() x+b交y轴于点D.
x+b交y轴于点D.

(1)求点D的坐标;
(2)把直线BD沿x轴翻折,交抛物线第二象限图象上一点E,过点E作x轴垂线,垂足为点F,求AF的长;
(3)在(2)的条件下,点P为抛物线上一点,若四边形BDEP为平行四边形,求m的值及点P的坐标.
【答案】(1)D(0,﹣2);(2)AF=1;(3)m=3,P(2,5).
【解析】试题分析:(1)由点的直线上,点的坐标符合函数解析式,代入即可;
(2)先求出OB,OD再利用锐角三角函数求出BF=2EF,由它建立方程4-t=2×[-![]() (t+m)(t-4)],求解即可;
(t+m)(t-4)],求解即可;
(3)先判断出△PEQ≌△DBO,表示出点P(t+4,-![]() (t+m)(t-4))+2),再利用它在抛物线y=-
(t+m)(t-4))+2),再利用它在抛物线y=-![]() (t+m)(t-4)上求解.
(t+m)(t-4)上求解.
试题解析:(1)∵抛物线y=-![]() (x+m)(x-4)(m>0)交x轴于点A、B(A左B右)
(x+m)(x-4)(m>0)交x轴于点A、B(A左B右)
当y=0时,0=-![]() (x+m)(x-4),
(x+m)(x-4),
∴x1=-m,x2=4
∴A(-m,0),B(4,0)
∵点B在直线y=![]() x+b上,
x+b上,
∴4×![]() +b=0,b=-2
+b=0,b=-2
∴直线y=![]() x-2,
x-2,
当x=0时y=-2
∴D(0,-2),
(2)设E(t,-![]() (t+m)(t-4)),
(t+m)(t-4)),
∵EF⊥x轴,
∴∠EFO=90° EF∥y轴,
∴F(t,0),
由(1)可知D(0,-2)B(4,0),
∴OD=2 OB=4,
∴在Rt△BDO中,tan∠DBO=![]() ,
,
∵直线BD沿x轴翻折得到BE,
∴∠DBO=∠EBF,
∴tan∠DBO=tan∠EBF,
∴tan∠EBF=![]() ,
,
∴![]() ,
,
∴BF=2EF,
∴EF=-![]() (t+m)(t-4)BF=4-t
(t+m)(t-4)BF=4-t
∴4-t=2×[-![]() (t+m)(t-4)]
(t+m)(t-4)]
∴t+m=1,
∴AF=t-(-m)
∴AF=1,
(3)如图,
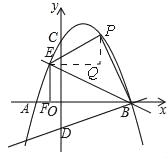
过点E作x轴的平行线,过点P作y轴的平行线交于点Q
设EP交y轴于点M
∵四边形BDEP是平行四边形
∴EP∥DB EP=DB
∵EP∥DB PQ∥y轴,
∴∠EMD=∠ODB∠EMD=∠EPQ,
∴∠ODB=∠EPQ,
∵∠PQE=∠DOB=90° EP=BD,
∴△PEQ≌△DBO,
∴PQ=OD=2 EQ=OB=4,
∵E(t,-![]() (t+m)(t-4)),
(t+m)(t-4)),
∴P(t+4,-![]() (t+m)(t-4)+2),
(t+m)(t-4)+2),
∵P(t+4,-![]() (t+m)(t-4))+2)在抛物线 y=-
(t+m)(t-4))+2)在抛物线 y=-![]() (t+m)(t-4)上
(t+m)(t-4)上
∴-![]() (t+4+m)(t+4-4)=-
(t+4+m)(t+4-4)=-![]() (t+m)(t-4)+2
(t+m)(t-4)+2
∵t+m=1,
∴t=-2,
∵t+m=1,
∴m=3,
∴-![]() (t+m)(t-4)+2=5,
(t+m)(t-4)+2=5,
∴P(2,5)