题目内容
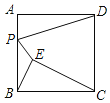
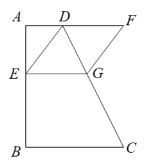
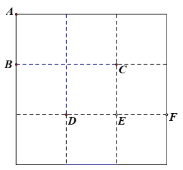
【题目】如图,在3![]() 3的正方形网格中,点A、B、C、D、E、F都是格点.
3的正方形网格中,点A、B、C、D、E、F都是格点.
(1)从A、D、E、F四点中任意取一点,以所取点及B、C为顶点画三角形,那么所画三角形是等腰三角形的概率是 .
(2)从A、D、E、F四点中任意取两点,以所取两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率.(请用“画树状图”或“列表”等方式写出分析过程)
【答案】(1)![]() ;(2)见解析,
;(2)见解析,![]()
【解析】
(1)找出从A、D、E、F四点中任意取一点组成等腰三角形的个数,再根据概率公式即可得出结论;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所画四边形是平行四边形的情况,然后利用概率公式求解即可求得答案.
(1)从A、D、E、F四点中任意取一点,以所取点及B、C为顶点可以画4个三角形,那么所画三角形是等腰三角形的有1个,故所画三角形是等腰三角形的概率是:![]()
故答案为:![]()
(2)用“树状图”或利用表格列出所有可能的结果:

∵共有12种等可能情况,其中满足要求的有4种
∴所画的四边形是平行四边形的概率P=![]()

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目