题目内容
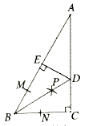
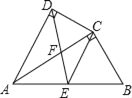
【题目】如图,四边形ABCD中,AC平分∠BAD,∠ADC=∠ACB=90°,E为AB的中点,AC与DE交于点F.
(1)求证:CE∥AD;
(2)求证:AC2=ABAD;
(3)若AC=![]() ,AB=8,求
,AB=8,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)欲证明CE∥AD,只要证明∠ACE=∠CAD即可;
(2)由AC平分∠DAB得∠DAC=∠CAB,加上∠ADC=∠ACB=90°可迅速得出结论;
(3)证明△AFD∽△CFE相似.
解:(1)∵E为AB中点,∠ACB=90°
∴CE=![]() AB=AE,
AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(2)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴![]()
∴AC2=ABAD;
(3)由(2)证得,AC2=ABAD,
∵AC=![]() ,AB=8,
,AB=8,
∴![]()
∵∠ACB=90°,E为AB的中点,
∴CE=![]() AB=4,
AB=4,
∵CE∥AD
∴△AFD∽△CFE,
∴![]()

练习册系列答案
相关题目