Question

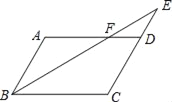
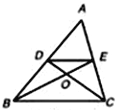
【题目】如图，在△ABC中，中线BE，CD相交于点O，连接DE，下列结论： ①=； ②=；③=；④=.其中正确的个数有（ ）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】

①根据三角形的中位线得出DE∥BC，DE=BC，根据平行线的性质得出相似，根据相似三角形的性质求出即可．

②由BE、CD是△ABC的中线，可得DE是△ABC的中位线，然后由三角形中位线的性质，可得△ODE∽△OCB，得出SOCB =4S△ODE.

③由BE、CD是△ABC的中线，可得DE是△ABC的中位线，然后由三角形中位线的性质，可得△ODE∽△OCB，再根据相似三角形的性质求出即可.

④由BE、CD是△ABC的中线，得出O是△ABC的重心，根据重心性质可得BO=2OE,△ABC的高=3△BOC的高，且△ABC与△BOC同底（BC）得出S△ABC =3S△BOC，由②和③知，S△ODE= S△COB，S△ADE = S△BOC，所以=．

①∵BE和CD是△ABC的中线，

∴DE=BC,DE∥BC，

∴DE：BC=,△DOE∽△COB，

∴OD:OC=DE:BC=，

故答案①正确.

②∵BE、CD是△ABC的中线，

∴DE∥BC,DE=12BC，AE=EC，

∴△ODE∽△OCB, SOCB =4S△ODE，

∴=

故答案②是错的.

③∵BE、CD是△ABC的中线，

∴DE∥BC,DE=BC，AE=EC，AD=DB

∴△ODE∽△OCB，=,

∴=，

∴==.

故答案③正确.

④∵△ABC的中线BE与CD交于点O.∴点O是△ABC的重心，根据重心性质，BO=2OE，△ABC的高=3△BOC的 高，且△ABC与△BOC同底（BC）∴S△ABC =3S△BOC，由②和③知，S△ODE= S△COB，S△ADE = S△BOC，∴ =．故④正确．

综上，①③④正确．故答案选C.