Question

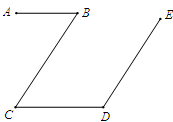
如图，已知∠A＝∠C，∠1＋∠2＝180°，试问：∠B与∠F有什么关系？为什么？

解：∠B＝∠F，理由如下：
∵∠A＝∠C
∴         ∥            （                ）
∴∠BDC＝∠B               （                ）
∵∠1＋∠2＝180°
且∠1＋∠3                 （                 ）
∴∠3＋∠2＝180°
∴           ∥          （                 ）
∴∠BDC＝                 （                 ）
∴∠B＝∠F                 （                 ）

Answer 1

∠B＝∠F，理由如下：
∵∠A＝∠C
∴ AB ∥ CD            （内错角相等，两直线平行）
∴∠BDC＝∠B           （两直线平行，内错角相等）
∵∠1＋∠2＝180°
且∠1＝∠3             （对顶角相等）
∴∠3＋∠2＝180°
∴ EF ∥ BD            （同旁内角互补，两直线平行）
∴∠BDC＝∠F
∴∠B＝∠F             （等量代换）

试题分析：根据平行线的判定和性质结合对顶角相等依次分析即可得到结果.
∠B＝∠F，理由如下：
∵∠A＝∠C
∴ AB ∥ CD            （内错角相等，两直线平行）
∴∠BDC＝∠B           （两直线平行，内错角相等）
∵∠1＋∠2＝180°
且∠1＝∠3             （对顶角相等）
∴∠3＋∠2＝180°
∴ EF ∥ BD            （同旁内角互补，两直线平行）
∴∠BDC＝∠F
∴∠B＝∠F             （等量代换）
点评：本题属于基础应用题，只需学生熟练掌握平行线的判定和性质，即可完成.