题目内容
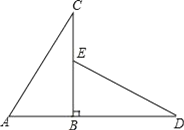
【题目】如图,E、F是矩形ABCD边BC上的两点,AF=DE.
(1)求证:BE=CF;
(2)若∠1=∠2=30°,AB=5,FC=2,求矩形ABCD的面积(结果保留根号).

【答案】(1)见解析;(2)![]()
【解析】
(1)首先证明Rt△ABF≌Rt△DCE,从而可得到BF=CE,然后由等式的性质进行证明即可;
(2)先依据含30°直角三角形的性质求得AF的长,然后依据勾股定理求得BF的长,从而可求得BC的长,最后,依据矩形的面积公式求解即可.
解:(1)∵矩形ABCD中∠B=∠C=90°,AB=CD.
又∵AF=DE
∴Rt△ABF≌Rt△DCE(HL),
∴BF=CE.
∴BF-EF=CE-EF,即BE=CF;
(2)∵Rt△ABF中,∠2=30°,
∴AF=2AB=10.
∴BF=![]() ,
,
∴BC=BF+FC=![]() ,
,
∴矩形ABCD的面积=ABBC=5(![]() )=
)=![]()

练习册系列答案
相关题目