题目内容
【题目】如图,在四边形![]() 中,
中, ![]() ,
,![]() 延长
延长![]() 至点
至点![]() ,连接
,连接![]() ,且
,且![]() 交
交![]() 于点
于点![]() ,
,![]() 和
和![]() 的角平分线相交于点
的角平分线相交于点![]() .
.

(1)求证:①![]() ;②
;②![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,
,![]() 请你探究
请你探究![]() 和
和![]() 之间的数量关系.
之间的数量关系.
【答案】(1)①见解析,②见解析;(2)65°;(3)![]() ,见解析.
,见解析.
【解析】
(1)①根据平行线的性质与判定证明即可;②过点P作PQ∥AB,则∠EAP=∠APQ,再根据平行线的性质证明即可;
(2)由AD∥BC,AB∥CD,可得∠EAD=∠B=70°,∠ECD=∠E=60°,再根据角平分线的性质解答即可;
(3)过点F作FH∥AB,根据平行线的性质以及角的和差关系解答即可.
(1)证明:①∵AD∥BC,∴∠EAD=∠B,
∵∠B=∠D,∴∠EAD=∠D,
∴AB∥CD;
②过点P作PQ∥AB,则∠EAP=∠APQ,
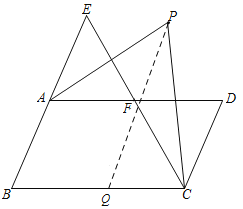
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵∠EAP=![]() ∠EAD,∠DCP=
∠EAD,∠DCP=![]() ∠ECD,
∠ECD,
∴![]() ∠EAD+
∠EAD+![]() ∠ECD=∠APC;
∠ECD=∠APC;
(2)由(1)知AD∥BC,AB∥CD,
∴∠EAD=∠B=70°,∠ECD=∠E=60°,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠APC=![]() (70°+60°)=65°;
(70°+60°)=65°;
(3)过点F作FH∥AB,则∠EAD=∠AFH,
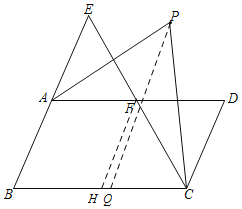
∵AB∥CD,
∴FH∥CD,
∴∠ECD=∠CFH,
∴∠EAD+∠ECD=∠AFH+∠CFH=∠AFC=∠EFD,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠EFD=2∠APC,
∵∠APC=m°,∠EFD=n°,
∴m=![]() n.
n.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目