题目内容
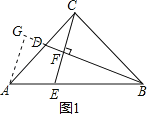
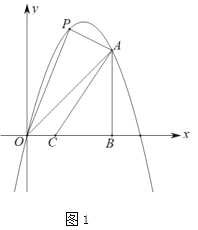
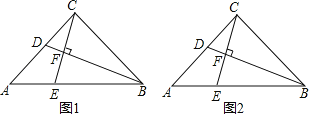
【题目】如图1,△ABC为等腰直角三角形,∠ACB=90°,AC=BC,点D和E分别是AC、AB上的点,CE⊥BD,垂足为F
(1)![]()
①求证:D为AC的中点;②计算![]() 的值.
的值.
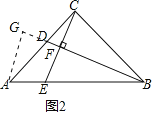
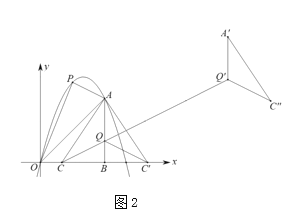
(2)若![]() ,如图2,则
,如图2,则![]() = (直接写出结果,用k的代数式表示)
= (直接写出结果,用k的代数式表示)
【答案】(1)①见解析;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①先证明△CDF∽△BDC,再利用相似的性质即可解答
②过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,得到![]() ,再利用勾股定理求出CF,BD,即可解答
,再利用勾股定理求出CF,BD,即可解答
(2)根据题意可知△CDF∽△BDC,再利用相似的性质求出![]() =k﹣1,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,得到AG=(k﹣1)CF,GD=(k﹣1)FD,再根据勾股定理即可解答
=k﹣1,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,得到AG=(k﹣1)CF,GD=(k﹣1)FD,再根据勾股定理即可解答
(1)①证明:∵∠ACB=90°,CE⊥BD,
∴∠BCD=∠CFD=90°.
∴∠BCF=∠CDF(同角的余角相等).
∴△CDF∽△BDC.
∴![]() .
.
∵![]() ,AC=BC,
,AC=BC,
∴![]() .
.
∴D为AC的中点;
②如图1,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,
∴△ADG∽△CDF.
∴![]() .
.
∴AG=CF,GD=FD.
在直角△CFD中,CF=2DF,CD2=DF2+CF2,易得CF=![]() CD.
CD.
在直角△BCD中,BC=2CD,BD2=CD2+BC2,易得BD=![]() CD.
CD.
由tan∠EBF=tan∠ABG知,![]() .
.
∴![]() .
.
(2)∵∠ACB=90°,CE⊥BD,
∴∠BCD=∠CFD=90°.
∴∠BCF=∠CDF(同角的余角相等).
∴△CDF∽△BDC.
∴![]() .
.
∵![]() ,AC=BC,
,AC=BC,
∴![]() .
.
∴![]() =k﹣1;
=k﹣1;
如图2,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,
∴△ADG∽△CDF.
∴![]() =k﹣1.
=k﹣1.
∴AG=(k﹣1)CF,GD=(k﹣1)FD.
在直角△CFD中,CF=kDF,CD2=DF2+CF2,易得CF=![]() .
.
在直角△BCD中,BC=kCD,BD2=CD2+BC2,易得BD=![]() CD.
CD.
由tan∠EBF=tan∠ABG知,![]() .即
.即![]()
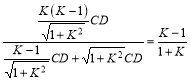 .
.
∴![]() .
.
故答案是:![]() .
.