题目内容
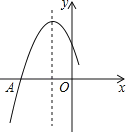
【题目】如图.在平面直角坐标系中.抛物线y=![]() x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
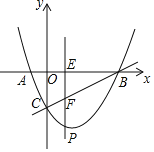
(1)求该抛物线的表达式;
(2)当线段EF,PF的长度比为1:2时,请求出m的值;
(3)是否存在这样的m,使得△BEP与△ABC相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)m=2或4;(3)存在,m的值为0或3.
;(2)m=2或4;(3)存在,m的值为0或3.
【解析】
(1)把点A、点C的坐标代入抛物线表达式,即可求解;
(2)设点E的坐标为(m,0),则点F的坐标为(m,![]() m﹣2),PE=2EF,即:
m﹣2),PE=2EF,即:![]() m﹣2
m﹣2![]() m2
m2![]() m+2=2(2
m+2=2(2![]() m),即可求解;
m),即可求解;
(3)当△BEP与△ABC相似,分∠EPB=∠CAB或∠EPB=∠ABC两种情况,求解即可.
抛物线过点C,则其表达式为:y![]() x2+bx﹣2,
x2+bx﹣2,
将点A坐标代入上式得:0![]() b﹣2,
b﹣2,
解得:b![]() ,
,
故:抛物线的表达式为:y![]() x2
x2![]() x﹣2;
x﹣2;
设直线BC过点C(0,﹣2),设其表达式为:y=kx﹣2,
将点B坐标代入上式得:0=4k﹣2,
解得:k![]() ,则直线BC的表达式为:y
,则直线BC的表达式为:y![]() x﹣2,
x﹣2,
同理直线AC的表达式为:y=﹣2x﹣2,
设点E的坐标为(m,0),则点F的坐标为(m,![]() m﹣2),
m﹣2),
当线段EF,PF的长度比为1:2时,即:PE=2EF,则:![]() m﹣2
m﹣2![]() m2
m2![]() m+2=2(2
m+2=2(2![]() m),解得:m=2或4;
m),解得:m=2或4;
直线BC的表达式为:y![]() x﹣2,直线AC的表达式为:y=﹣2x﹣2,则:BC⊥AC,当△BEP与△ABC相似,则∠EPB=∠CAB,或∠EPB=∠ABC,
x﹣2,直线AC的表达式为:y=﹣2x﹣2,则:BC⊥AC,当△BEP与△ABC相似,则∠EPB=∠CAB,或∠EPB=∠ABC,
即:tan∠EPB=tan∠CAB,或tan∠EPB=tan∠ABC,
当tan∠EPB=tan∠CAB时,即: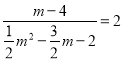 ,
,
解得:m=0或4(舍去m=4),
同理,当tan∠EPB=tan∠ABC,m=3或4(舍去m=4).
故存在,m的值为0或3.