题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点,过二次函数
为坐标原点,过二次函数![]() 图象上的点
图象上的点![]() ,作
,作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() .
.
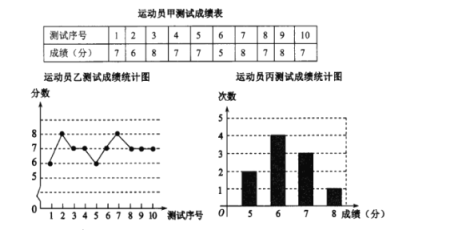
(1)如图1,![]() 为线段
为线段![]() 上方抛物线上的一点,在
上方抛物线上的一点,在![]() 轴上取点
轴上取点![]() ,点
,点![]() 、
、![]() 为
为![]() 轴上的两个动点,点
轴上的两个动点,点![]() 在点
在点![]() 的上方且
的上方且![]() 连接
连接![]() ,当四边形
,当四边形![]() 的面积最大时,求
的面积最大时,求![]() 的最小值.
的最小值.
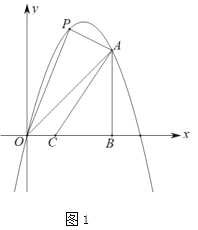
(2)如图2,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,
翻折,![]() 点的对应点为
点的对应点为![]() ,将
,将![]() 沿射线
沿射线![]() 平移
平移![]() 个单位得
个单位得![]() ,在抛物线上取一点
,在抛物线上取一点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 点的坐标.
点的坐标.
【答案】(1)![]() (2)(7,3),(
(2)(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() ).
).
【解析】
(1)把四边形PACO沿OA分成△OAP与△OAC,由于△OAC三边确定,面积为定值,故△OAP面积最大时四边形面积也最大.过点P作x轴垂线交OA于D,设点P横坐标为t,则能用t表示PD的长,进而得到△OAP关于t的二次函数关系式,用公式法可求得t=![]() 时△OAP面积最大,即求得此时点P坐标.把点P向下平移1个单位得P',易证四边形MNP'P是平行四边形,所以PM=P'N.过点O作经过第二、四象限的直线l,并使直线l与x轴夹角为60°,过点N作NG⊥直线l于点G,则由30°角所对直角边等于斜边一半可知NG=
时△OAP面积最大,即求得此时点P坐标.把点P向下平移1个单位得P',易证四边形MNP'P是平行四边形,所以PM=P'N.过点O作经过第二、四象限的直线l,并使直线l与x轴夹角为60°,过点N作NG⊥直线l于点G,则由30°角所对直角边等于斜边一半可知NG=![]() NO.所以PM+MN+
NO.所以PM+MN+![]() NO可转化为P'N+NG+1,易得当点P'、N、G在同一直线上最小.把PD延长交直线l于点F,构造特殊Rt△P'FG和Rt△OEF,利用点P坐标和30°、60°的三角函数即可求得P'G的长.
NO可转化为P'N+NG+1,易得当点P'、N、G在同一直线上最小.把PD延长交直线l于点F,构造特殊Rt△P'FG和Rt△OEF,利用点P坐标和30°、60°的三角函数即可求得P'G的长.
(2)由点B、C、Q的坐标求CQ的长和点C'坐标;过点Q'作x轴的垂线段Q'H,易证△CBQ∽△CHQ',故有![]() ,求得CH、HQ'的长即求得点Q'坐标,进而得到向右向上平移的距离,求得点A'、C'的坐标.求直线CQ解析式,设CQ上的点M横坐标为m,用两点间距离公式可得用m表示A'M和C'M的长.因为△A'MC'是等腰三角形,分三种情况讨论,得到关于m的方程,求解即求得相应的m的值,进而得点M坐标.
,求得CH、HQ'的长即求得点Q'坐标,进而得到向右向上平移的距离,求得点A'、C'的坐标.求直线CQ解析式,设CQ上的点M横坐标为m,用两点间距离公式可得用m表示A'M和C'M的长.因为△A'MC'是等腰三角形,分三种情况讨论,得到关于m的方程,求解即求得相应的m的值,进而得点M坐标.
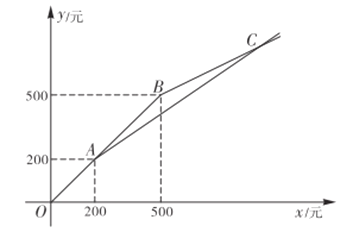
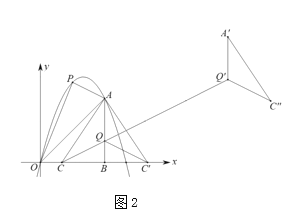
解:(1)如图1,过点O作直线l,使直线l经过第二、四象限且与x轴夹角为60°;
过点P作PF⊥x轴于点E,交OA于点D,交直线l于点F;在PF上截取PP'=1;过点N作NG⊥直线l于点G
∵A(3,3),AB⊥x轴于点B
∴直线OA解析式为y=x,OB=AB=3
∵C(1,0)
∴S△AOC=![]() OCAB=
OCAB=![]() ×1×3=
×1×3=![]() ,是定值
,是定值
设P(t,t2+4t)(0<t<3)
∴D(t,t)
∴PD=t2+4tt=t2+3t
∴S△OAP=S△OPD+S△APD=![]() PDOE+
PDOE+![]() PDBE=
PDBE=![]() PDOB=
PDOB=![]() (t23t)
(t23t)
∴t=![]() =
=![]() 时,S△OAP最大
时,S△OAP最大
此时,S四边形PACO=S△AOC+S△OAP最大
yP=(![]() )2+3×
)2+3×![]() =
=![]()
∴P(![]() ,
,![]() )
)
∴P'E=PEPP'=![]() 1=
1=![]() ,即P'(
,即P'(![]() ,
,![]() )
)
∵点M、N在y轴上且MN=1
∴PP'=MN,PP'∥MN
∴四边形MNP'P是平行四边形
∴PM=P'N
∵∠NGO=90°,∠NOG=90°60°=30°
∴Rt△ONG中,NG=![]() NO
NO
∴PM+MN+![]() NO=P'N+NG+1
NO=P'N+NG+1
∴当点P'、N、G在同一直线上,即P'G⊥直线l时,PM+MN+![]() NO=P'G+1最小
NO=P'G+1最小
∵OE=![]() ,∠EOF=60°,∠OEF=90°
,∠EOF=60°,∠OEF=90°
∴Rt△OEF中,∠OFE=30°,tan∠EOF=![]() =
=![]()
∴EF=![]() OE=
OE=![]()
∴P'F=P'E+EF=![]() +
+![]()
∴Rt△P'GF中,P'G=![]() P'F=
P'F=![]()
∴P'G+1=![]() +1=
+1=![]()
∴PM+MN+![]() NO的最小值为
NO的最小值为![]()
(2)延长A'Q'交x轴于点H
∵C(1,0),Q(3,1),QB⊥x轴于点B
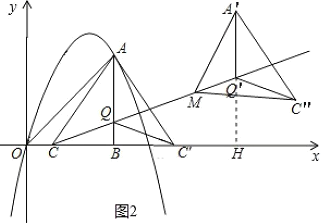
∴CB=2,BQ=1
∴CQ=![]() =
=![]()
∵△AQC沿直线AB翻折得△AQC'
∴B(3,0)是CC'的中点
∴C'(5,0)
∵平移距离QQ'=3![]()
∴CQ'=CQ+QQ'=4![]()
∵QB∥Q'H
∴△CBQ∽△CHQ'
∴![]()
∴CH=4CB=8,yQ'=HQ'=4BQ=4
∴xQ'=OC+CH=1+8=9
∴Q'(9,4)
∴点Q(3,1)向右平移6个单位,向上平移3个单位得到点Q'(9,4)
∴A'(9,6),C'(11,3)
∴A'C'=![]()
设直线CQ解析式为y=kx+b
∴![]()
解得: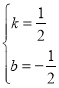
∴直线CQ:y=![]() x
x![]()
设射线CQ上的点M(m,![]() m
m![]() )(m>1)
)(m>1)
∴A'M2=(9m)2+(6![]() m+
m+![]() )2=(9m)2+(
)2=(9m)2+(![]() )2
)2
C'M2=(11m)2+(3![]() m+
m+![]() )2=(11m)2+(
)2=(11m)2+(![]() )2
)2
∵△A'MC'是等腰三角形
故①若A'M=A'C',则(9m)2+(![]() )2=13
)2=13
解得:m1=7,m2=![]()
∴M(7,3)或(![]() ,
,![]() )
)
②若C'M=A'C',则(11m)2+(![]() )2=13
)2=13
解得:m1=![]() ,m2=13
,m2=13
∴M(![]() ,
,![]() )或(13,6)
)或(13,6)
③若A'M=C'M,则(9m)2+(![]() )2=(11m)2+(
)2=(11m)2+(![]() )2
)2
解得:m=10
∴M(10,![]() )
)
综上所述,点M坐标为(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() ).
).

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
水银柱的长度x(cm) | 4.2 | … | 8.2 | 9.8 |
体温计的读数y(℃) | 35.0 | … | 40.0 | 42.0 |
(1)求y关于x的函数关系式(不需要写出函数的定义域)
(2)用该体温计测体温时,水银柱的长度为6.6cm,求此时体温计的读数.
![]()