题目内容
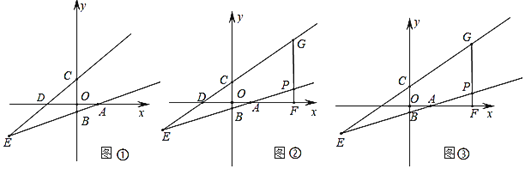
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,则下列结论:
①abc>0
②a﹣b+c<0;
③2a+b+c>0;
④x(ax+b)≤a+b;
其中正确的有_____
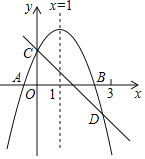
【答案】②③④
【解析】
根据二次函数系数与图像的关系即可求解.
∵对称轴x=1,
∴b=﹣2a,
由图可知c>0,a<0,
①abc<0,不正确;
②当x=﹣1时,y<0,
∴a﹣b+c<0;正确;
③2a+b+c=2a﹣2a+c=c>0;正确;
④当x=1时,函数y有最大值a+b+c,
∴x(ax+b)+c≤a+b+c,
∴x(ax+b)≤a+b;正确;
故答案为②③④;

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校![]() 班和
班和![]() 班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
![]() 班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据.
班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据.
平均数 | 中位数 | 众数 | 极差 | 方差 |
|
|
|
|
|
![]() 班的同学还将自主复习时间分为四大类:第一类为时间小于
班的同学还将自主复习时间分为四大类:第一类为时间小于![]() 分钟以下,第二类为时间大于或等于
分钟以下,第二类为时间大于或等于![]() 分钟且小于
分钟且小于![]() 分钟,第三类为时间大于或等于
分钟,第三类为时间大于或等于![]() 分钟且小于
分钟且小于![]() 分钟,第四类为时间大于或等于
分钟,第四类为时间大于或等于![]() 分钟,并得到如下的扇形图.
分钟,并得到如下的扇形图.

(1)在扇形图中,第一类所对的圆心角度数 .
(2)写出![]() 班被调查同学的以下特征数.
班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
|
|
|
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些,其理由为(至少两条):
.
【题目】现实社会中,塑料袋仍然是白色污染的一部分,为了解塑料袋的使用情况,某校八年级环保小组随机抽取“幸福小区”40户居民家庭,记录了这些家庭某个月丢弃塑料袋的数量(单位:个)如下:
29 39 35 39 39 27 33 35 31 31
32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38
29 39 35 33 39 39 38 42 37 32
请根据上述数据,解答以下问题:
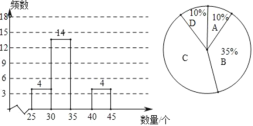
(1)若数据为x,按“组距为5”列出了如下的频数分布表,请将表中空缺的部分补充完整,并补全频数分布直方图;
分组 | 频数 |
A:25≤x<30 | 4 |
B:30≤x<35 | 14 |
C:35≤x<40 | |
D:40≤x<45 | 4 |
合计 | 40 |
(2)根据(1)中的直方图可以看出,这40户居民家庭这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,画出了如图所示的扇形统计图,请求出C组对应的扇形圆心角的度数;
(4)若该小区共有1000户居民家庭,请你估计每月丢弃的塑料袋数量不小于30个的家庭户数.