Question

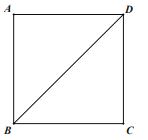
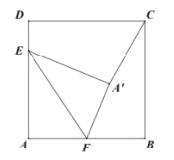
【题目】如图，在边长为的正方形中，点为的靠近点的四等分点，点为的中点， 将沿着翻折得，连接，则点到的距离为（ 　）

A.B.C.D.

Answer 1

【答案】C

【解析】

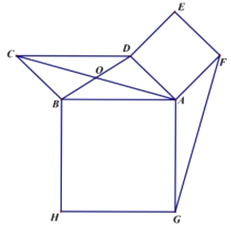
过点A'作GH∥AD，交AB、CD于点G、H，过点E作EK⊥GH，垂足为点K，先通过折叠可得A'E= AE=3，A'F= AF=2，∠A'=∠A=90°，再结合∠EKG=∠G=90°，证得△A'KE∽△FGA'，根据相似三角形的性质可得相似比为3:2，故可设A'K=3x， FG=2x，进而表示出EK和A'G的长，再根据相似比列出方程求出x，即可求得A'G、A'H的长，再用勾股定理求得A'C的长，最后根据等积法求得点D到的距离即可．

解：如图，过点A'作GH∥AD，交AB、CD于点G、H，过点E作EK⊥GH，垂足为点K，

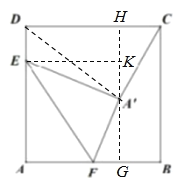
则四边形AGKE、DEKH、BGHC均为矩形，

由题意可知DE=1，AE=3，AF=BF=2，DC=4，∠A=90°，

∵折叠，

∴A'E= AE=3，A'F= AF=2，∠A'=∠A=90°，

又∵∠EKG=∠G=90°，

∴△A'KE∽△FGA'，

∴，

设A'K=3x，则FG=2x，

在矩形AGKE中，AE=KG=3，EK=AG=2+2x，

∴A'G=KG- A'K=3-3x

∴

解得x=，

∴A'H=HG- A'G=4-（3-3×）=，

又∵HC=CD-DK=4-（2+2×）=，

∴在Rt△A'HC中，A'C=，

设点D到A'C的距离为h，

则S△A'DC=A'C×h=CD×A'H，

∴A'C×h=CD×A'H，

∴，

解得h=，

故选：C．