题目内容
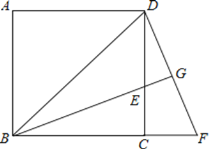
【题目】为了节省材料，某农场主利用围墙（围墙足够长）为一边，用总长为80m的篱笆围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等，则能围成的矩形区域ABCD的面积最大值是___m2．
【答案】300．
【解析】
根据三个矩形面积相等，得到矩形AEFD面积是矩形BCFE面积的2倍，可得出AE＝2BE，设BE＝a，则有AE＝2a，表示出a与2a，进而表示出y与x的关系式，并求出x的范围即可；再利用二次函数的性质求出面积S的最大值即可．
如图，
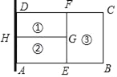
∵三块矩形区域的面积相等，
∴矩形AEFD面积是矩形BCFE面积的2倍，
∴AE＝2BE，
设BC＝x，BE＝FC＝a，则AE＝HG＝DF＝2a，
∴DF+FC+HG+AE+EB+EF+BC＝80，即8a+2x＝80，
∴a＝﹣
x+10，3a＝﹣
x+30，
∴矩形区域ABCD的面积S＝（﹣x+30）x＝﹣x2+30x，
∵a＝﹣x+10＞0，
∴x＜40，
则S＝﹣x2+30x（0＜x＜40）；
∵S＝﹣x2+30x＝﹣（x﹣20）2+300（0＜x＜40），且二次项系数为﹣＜0，
∴当x＝20时，S有最大值，最大值为300m2．
故答案为：300．
练习册系列答案
阅读快车系列答案
相关题目
