题目内容
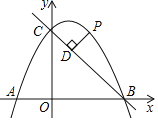
【题目】如图,直线y=﹣x+4与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且OA=![]() OB,抛物线y=ax2+bx+4经过A,B,C三点.
OB,抛物线y=ax2+bx+4经过A,B,C三点.
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作PD⊥BC,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值.
【答案】(1)y=﹣![]() x2+x+4;(2)PD=﹣
x2+x+4;(2)PD=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,,PD有最大值,最大值为
,,PD有最大值,最大值为![]() .
.
【解析】
(1)先求出点A、B的坐标,再利用待定系数法求解即可;
(2)先求出C、P的坐标,由此得到线段CP的长度,根据平行线的性质得![]() ,解直角三角形即可求出PD的表达式,利用二次函数的性质求出PD的最大值即可.
,解直角三角形即可求出PD的表达式,利用二次函数的性质求出PD的最大值即可.
(1)在y=﹣x+4中,当x=0时,y=4;当y=0时,x=4,
∴B(4,0),C(0,4),
∴OB=OC=4,
∴OA=![]() OB=2,
OB=2,
即A(﹣2,0),
把A(﹣2,0),B(4,0)代入y=ax2+bx+4中,得
![]() ,解得
,解得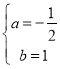 ,
,
抛物线的解析式为:y=﹣![]() x2+x+4;
x2+x+4;
(2)过P作PF∥y轴,交BC于F,
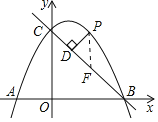
在Rt△OBC中,∵OB=OC=4,∴∠OCB=45°,
∴∠PFD=45°,
∴PD=![]() PF,
PF,
由P(m,﹣![]() m2+m+4),F(m,-m+4),得:PF=﹣
m2+m+4),F(m,-m+4),得:PF=﹣![]() m2+2m,
m2+2m,
∴PD=![]() (﹣
(﹣![]() m2+2m)
m2+2m)
=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,其中,0<m<4,
,其中,0<m<4,
∵﹣![]() <0,
<0,
∴当m=2时,PD有最大值,最大值为![]() .
.

练习册系列答案
相关题目